С. Берлов
Задача №1. В треугольнике $ABC$ стороны $AB$ и $BC$ равны. Точка $D$ внутри треугольника такова, что угол $ADC$ вдвое больше угла $ABC$. Докажите, что удвоенное расстояние от точки $B$ до прямой, делящей пополам углы, смежные с углом $ADC$, равно $AD+DC$. ( С. Берлов )
комментарий/решение(3) олимпиада
Задача №2. В выпуклом четырехугольнике $ABCD$ выполнены соотношения $AB = BD$; $\angle ABD = \angle DBC$. На диагонали $BD$ нашлась точка $K$ такая, что $BK = BC$. Докажите, что $\angle KAD = \angle KCD$. ( С. Берлов )
комментарий/решение(6) олимпиада
Задача №3. В Швамбрании некоторые города связаны двусторонними беспосадочными авиарейсами. Рейсы разделены между тремя авиакомпаниями, причём если какая-то авиакомпания обслуживает линию между городами А и Б, то самолёты других компаний между этими городами не летают. Известно, что из каждого города летают самолёты всех трёх компаний. Докажите, что можно, вылетев из некоторого города, вернуться в него, воспользовавшись по пути рейсами всех трёх компаний и не побывав ни в одном из промежуточных городов дважды. ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №4. В выпуклом четырехугольнике $ABCD$ углы $B$ и $D$ равны, $CD = 4BC$, а биссектриса угла $A$ проходит через середину стороны $CD$. Чему может быть равно отношение $AD/AB$? ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №5. Бизнесмен Борис Михайлович решил устроить с трактористом Васей гонки по шоссе. Поскольку его «Лексус» едет вдесятеро быстрее Васиного трактора, он дал Васе фору и выехал через час после Васи. После того, как Васин трактор проехал ровно половину запланированной трассы, у него отвалилась рессора, поэтому оставшуюся часть пути Вася проехал вдвое медленнее, чем первую. В результате встречи с Васиной рессорой Борису Михайловичу пришлось заехать в оказавшийся рядом сервис на 4 часа, после чего он продолжил путь вдвое медленнее, чем раньше. Докажите, что в результате он отстал от Васи не менее, чем на час. ( С. Берлов )
комментарий/решение(2) олимпиада
Задача №6. В треугольнике $ABC$ точки $M$ и $N$ — середины сторон $AC$ и $AB$ соответственно. На медиане $BM$ выбрана точка $P$, не лежащая на $CN$. Оказалось, что $PC = 2PN$. Докажите, что $AP = BC$. ( С. Берлов )
комментарий/решение(3) олимпиада
Задача №7. Докажите, что для любого натурального числа $n > 1$ найдутся такие натуральные числа $a, b, c, d$, что $a+b = c+d = ab - cd = 4n$. ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №8. Внутри выпуклого четырехугольника $ABCD$, в котором $AB = CD$, выбрана точка $P$ таким образом, что сумма углов $PBA$ и $PCD$ равна 180 градусам. Докажите, что $PB+PC < AD$. ( С. Берлов )
комментарий/решение(2) олимпиада
Задача №9. Назовем четырехзначное число $x$ забавным, если каждую его цифру можно увеличить или уменьшить на 1 (при этом цифру 9 можно только уменьшать, а 0 — только увеличивать) так, чтобы в результате получилось число, делящееся на $x$. а) Найдите два забавных числа. б) Найдите три забавных числа. в) Существует ли четыре забавных числа? ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №10. Собственным делителем числа называется любой его натуральный делитель, кроме 1 и самого числа. С составным натуральным числом $a$ разрешается проделывать следующие операции: разделить на наименьший собственный делитель или прибавить любое натуральное число, делящееся на его наибольший собственный делитель. Если число получилось простым, то с ним ничего нельзя делать. Верно ли, что с помощью таких операций из любого составного числа можно получить число 2011? ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №11. 1000 различных положительных чисел записаны в ряд в порядке возрастания. Вася разбил эти числа на 500 пар соседних и нашел суммы чисел во всех парах. Петя разбил эти же числа на 500 пар таким образом, что между числами в каждой паре стоит ровно три других числа, и тоже нашел суммы чисел во всех парах. Докажите, что произведение сумм, найденных Петей, больше, чем произведение сумм, найденных Васей. ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №12. Существуют ли два многоугольника (не обязательно выпуклых), обладающих следующим свойством: прикладывая их друг к другу (без наложения), можно получить многоугольники с любым числом сторон от 3 до 100 включительно? ( И. Богданов, С. Волчёнков, С. Берлов )
комментарий/решение(1) олимпиада
Задача №13. Углы треугольника ABC удовлетворяют условию $2\angle A+\angle B = \angle C$. Внутри этого треугольника на биссектрисе угла $A$ выбрана точка $K$ такая, что $BK = BC$. Докажите, что $\angle KBC = 2\angle KBA$. ( С. Берлов )
комментарий/решение(2) олимпиада
Задача №14. 200 человек стоят по кругу. Каждый из них либо лжец, либо конформист. Лжец всегда лжет. Конформист, рядом с которым стоят два конформиста, всегда говорит правду. Конформист, рядом с которым стоит хотя бы один лжец, может как говорить правду, так и лгать. 100 из стоящих сказали: «Я — лжец», 100 других сказали: «Я — конформист». Найдите наибольшее возможное число конформистов среди этих 200 человек. ( Р. Женодаров, С. Берлов )
комментарий/решение(1) олимпиада
Задача №15. Из шахматной доски размером $13 \times 13$ вырезали две противоположные угловые клетки. На оставшейся части доски отметили несколько клеток. Докажите, что на отмеченные клетки можно поставить шахматных королей так, чтобы всего королей было не больше 47, и они били все пустые отмеченные клетки. Напомним, что шахматный король бьет все клетки, соседние с ним по вертикали, горизонтали и диагонали. ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №16. Диагонали выпуклого четырёхугольника $ABCD$ равны и пересекаются в точке $O$. Точка $P$ внутри треугольника $AOD $ такова, что $CD \parallel BP $ и $AB \parallel CP$. Докажите, что точка $P$ лежит на биссектрисе угла $AOD$. ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №17. В гандболе за победу дают 2 очка, за ничью — 1 очко, за поражение — 0 очков.14 гандбольных команд провели турнир, где каждая команда с каждой сыграла по одному разу. Оказалось, что никакие две команды не набрали поровну очков. Могло ли случиться, что каждая из команд, занявших первые три места, проиграла каждой из команд, занявших последние три места? ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №18. В выпуклом четырёхугольнике $ABCD$, в котором $AB = CD$, на сторонах $AB$ и $CD$ выбраны точки $K$ и $M$ соответственно. Оказалось, что $AM = KC$, $BM = KD$. Докажите, что угол между прямыми $AB$ и $KM$ равен углу между прямыми $KM$ и $CD$. ( С. Берлов )
комментарий/решение(2) олимпиада
Задача №19. На доске в строчку написано $n$ подряд идущих натуральных чисел в порядке возрастания. Под каждым из этих чисел написан его делитель, меньший этого числа и больший 1. Оказалось, что эти делители тоже образуют строчку подряд идущих натуральных чисел в порядке возрастания. Докажите, что каждое из исходных чисел больше, чем $\frac{{{n}^{k}}}{{{p}_{1}}{{p}_{2}}\ldots {{p}_{k}}}$, где $p_1$, $p_2$, $\dots $, $p_k$ — все простые числа, меньшие $n$. ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №20. На стороне $AC$ треугольника $ABC$ выбрана точка $D$ такая, что $BD = AC$. Медиана $AM$ этого треугольника пересекает отрезок $BD$ в точке $K$. Оказалось, что $DK = DC$. Докажите, что $AM+KM = AB$. ( С. Берлов )
комментарий/решение(2) олимпиада
Задача №21. Дан выпуклый пятиугольник $ABCDE$, причём прямая $BE$ параллельна прямой $CD$ и отрезок $BE$ короче отрезка $CD$. Внутри пятиугольника выбраны точки $F$ и $G$ таким образом, что $ABCF$ и $AGDE$ — параллелограммы. Докажите, что $CD = BE + FG$. ( С. Берлов, К. Кноп )
комментарий/решение(1) олимпиада
Задача №22. Дано 2014 попарно различных натуральных чисел таких, что произведение любых двух из них делится на сумму этих двух чисел. Докажите, что ни одно из данных чисел не может быть равно произведению шести попарно различных простых чисел. ( И. Рубанов, С. Берлов, В. Сендеров )
комментарий/решение(1) олимпиада
Задача №23. Назовём натуральное число $\textit{гористым}$, если в его записи есть не стоящая с краю цифра (называемая $\textit{вершиной}$), которая больше всех остальных, а все остальные цифры ненулевые и сначала нестрого возрастают (то есть каждая следующая цифра больше предыдущей или равна ей) до вершины, а потом нестрого убывают (то есть каждая следующая цифра меньше предыдущей или равна ей). Например, число 12243 — гористое, а числа 3456 и 1312 — нет. Докажите, что сумма всех стозначных гористых чисел — составное число. ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №24. Диагональ выпуклого 101-угольника будем называть главной, если по одну сторону от неё лежит 50, а по другую — 49 вершин. Выбрано несколько главных диагоналей, не имеющих общих концов. Докажите, что сумма длин этих диагоналей меньше суммы длин остальных главных диагоналей. ( И. Богданов, С. Берлов )
комментарий/решение(1) олимпиада
Задача №25. Серединные перпендикуляры к сторонам $AB$ и $BC$ выпуклого четырёхугольника $ABCD$ пересекают стороны $CD$ и $DA$ в точках $P$ и $Q$ соответственно. Оказалось, что $\angle APB = \angle BQC$. Внутри четырёхугольника выбрана точка $X$ такая, что $QX \parallel AB$ и $PX \parallel BC$. Докажите, что прямая $BX$ делит диагональ $AC$ пополам. ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №26. На столе лежит палочка длиной 10 см. Петя ломает её на две части и кладёт обе получившиеся палочки на стол. С одной из лежащих на столе палочек Вася проделывает ту же операцию, потом то же делает Петя и т.д., по очереди. Петя хочет, чтобы после 18 разломов все получившиеся палочки были короче 1 см. Вася хочет помешать Пете. Кто из них имеет возможность добиться своей цели независимо от действий соперника? ( И. Рубанов, С. Берлов )
комментарий/решение(1) олимпиада
Задача №27. На шахматной доске размером $20\times20$ расставлены 220 коней, которые бьют все свободные клетки. Докажите, что можно убрать 20 коней таким образом, чтобы оставшиеся кони били все свободные клетки. Напомним, что конь бьёт буквой «Г» (см. рисунок).
комментарий/решение(1) олимпиада
Задача №28. По кругу написаны 2015 положительных чисел. Сумма любых двух рядом стоящих чисел больше суммы обратных к двум следующим за ними по часовой стрелке. Докажите, что произведение всех этих чисел больше 1. ( С. Берлов, А. Голованов )
комментарий/решение(1) олимпиада
Задача №29. Натуральное число называется совершенным, если оно вдвое меньше суммы всех своих натуральных делителей: например, совершенным является число 6, так как $2\cdot 6 = 1+2+3+6$. Может ли сумма всех попарных произведений натуральных делителей совершенного числа $n$ делиться на $n^2$? ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №30. $CK$ — биссектриса треугольника $ABC$. На сторонах $BC$ и $AC$ выбраны точки $L$ и $T$ соответственно такие, что $CT = BL$ и $TL = BK$. Докажите, что треугольник $LTC$ подобен исходному. ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №31. В одной деревне живут рыцари, которые всегда говорят правду, и лжецы, которые всегда лгут. Путешественник каждому жителю деревни задал два вопроса: «Сколько в деревне рыцарей?» и «На сколько отличаются количества рыцарей и лжецов?». Путешественник знает, что в деревне есть хотя бы один рыцарь. Всегда ли по полученным ответам путешественник сможет узнать, кто из жителей деревни рыцарь, а кто — лжец? ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №32. Даны $2n$-значное натуральное число $a$ и натуральное число $k$. Числа $a$ и $ka$ записали на ленте и каждую из двух записей разрезали на двузначные числа, начиная с последних цифр (при этом числа $00$, $01$, $\ldots$, $09$ здесь тоже считаются двузначными; если в числе $ka$ оказалось нечетное количество цифр, к нему спереди приписали $0$). Оказалось, что у числа $a$ полученные двузначные числа строго убывают справа налево (от младших разрядов числа $a$ к старшим), а у числа $ka$ — строго возрастают. Докажите, что $k \geq n$. ( С. Берлов, О. Нечаева )
комментарий/решение(2) олимпиада
Задача №33. Решите в натуральных числах уравнение $(a^2,b^2)+(a,bc)+(b,ac)+(c,ab)=199.$ (Здесь $(x,y)$ — наибольший общий делитель). ( С. Берлов )
комментарий/решение(2) олимпиада
Задача №34. В квадрате $n \times n$ ($n > 2$) стоят ненулевые числа. Известно, что каждое число ровно в $k$ раз меньше, чем сумма всех чисел, стоящих с ним в одном "кресте" (т.е.\ в остальных $2n-2$ клетках той же строки и того же столбца) При каких $k$ такое возможно? ( С. Берлов, А. Храбров, Д. Ростовский )
комментарий/решение олимпиада
Задача №35. В выпуклом четырехугольнике $ABCD$ лучи $DA$ и $CB$ пересекаются в точке $Q$, а лучи $BA$ и $CD$ — в точке $P$. Оказалось, что $\angle AQB=\angle APD$. Биссектриса угла $\angle AQB$ пересекает стороны $AB$ и $CD$ четырехугольника в точках $X$ и $Y$ соответственно, а биссектриса $\angle APD$ пересекает стороны $AD$ и $BC$ в точках $Z$ и $T$ соответственно. Описанные окружности треугольников $ZQT$ и $XPY$ пересекаются в точке $K$ внутри четырехугольника. Докажите, что $K$ лежит на диагонали $AC$. ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №36. Расстановку фишек в клетках квадрата $n\times n$ назовем редкой, если в любом квадрате $2\times 2$ стоит не более 3 фишек. Сергей поставил в некоторые клетки доски по одной фишке так, что получилась редкая расстановка. Он заметил, однако, что если переставить любую фишку на любую свободную клетку, то перестановка перестанет быть редкой. При каких $n$ это возможно? ( С. Берлов )
комментарий/решение олимпиада
Задача №37. Дано натуральное число $n$. Известно, что существуют такие 2010 последовательных натуральных чисел, что ни одно из них не делится на $n$, но их произведение кратно $n$. Докажите, что существуют такие 2004 последовательных натуральных чисел, что ни одно из них не делится на $n$, но их произведение кратно $n$. ( С. Берлов )
комментарий/решение олимпиада
Задача №38. Даны два натуральных числа $a < b$. Докажите, что из любых $b$ последовательных натуральных чисел можно выбрать два числа, произведение которых делится на $ab$. ( С. Берлов )
комментарий/решение(4) олимпиада
Задача №39. Существует ли такое натуральное число, состоящее из нечётных цифр, причём цифр 1, 3, 5, 7, 9 в нём поровну, которое делится на любое 20-значное число, получаемое из него вычёркиванием цифр (ни вычеркиваемые, ни оставшиеся цифры не обязаны стоять подряд)? ( С. Берлов )
комментарий/решение олимпиада
Задача №40. Некоторое натуральное число $a$ разделили с остатком на числа 1, 2, 3, $\ldots$, 1000. Могло ли так случиться, что среди остатков ровно по 10 раз встретятся числа 0, 1, 2, 3, $\ldots$, 99? ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №41. В выпуклом четырёхугольнике $ABCD$ углы $A$ и $C$ равны $100^\circ$. На сторонах $AB$ и $BC$ выбраны точки $X$ и $Y$ соответственно так, что $AX = CY$. Оказалось, что прямая $YD$ параллельна биссектрисе угла $ABC$. Найдите угол $AXY$. ( С. Берлов, А. Кузнецов )
комментарий/решение(1) олимпиада
Задача №42. В выпуклом четырёхугольнике $ABCD$ биссектриса угла $B$ проходит через середину стороны $AD$, а $\angle C = \angle A+\angle D$. Найдите угол $ACD$. ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №43. Имеется клетчатая доска размером $2n \times 2n$. Петя поставил на неё ${(n+1)^2}$ фишек. Кот может одним взмахом лапы смахнуть на пол любую одну фишку или две фишки, стоящие в соседних по стороне или углу клетках. За какое наименьшее количество взмахов кот заведомо сможет смахнуть на пол все поставленные Петей фишки? ( С. Берлов, Н. Власова )
комментарий/решение(2) олимпиада
Задача №44. В треугольнике $ABC$ проведена медиана $BD$. Биссектрисы углов $ABD$ и $ACB$ перпендикулярны. Найдите наибольшее возможное значение угла $BAC$. ( С. Берлов )
комментарий/решение олимпиада
Задача №45. Дан прямоугольник $ABCD$. На луче $DC$ отложен отрезок $DK$, равный $BD$. Точка $M$ — середина отрезка $BK$. Докажите, что $AM$ — биссектриса угла $BAC$. ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №46. Вневписанная окружность треугольника $ABC$ касается его стороны $AB$ в точке $P$, а продолжений сторон $AC$ и $BC$ — в точках $Q$ и $R$ соответственно. Докажите, что если середина $PQ$ лежит на описанной окружности треугольника $ABC$, то и середина $PR$ тоже лежит на этой описанной окружности. ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №47. Дано натуральное число $n$. Известно, что существуют такие пять последовательных натуральных чисел, что ни одно из них не делится на $n$, но их произведение кратно $n$. Докажите, что существуют такие четыре последовательных натуральных числа, что ни одно из них не делится на $n$, но их произведение кратно $n$. ( С. Берлов )
комментарий/решение олимпиада
Задача №48. Окружность, концентрическая со вписанной окружностью треугольника $ABC$, пересекает стороны треугольника в шести точках, образующих выпуклый шестиугольник $A_1A_2B_1B_2C_1C_2$ (точки $A_1$ и $A_2$ лежат на стороне $BC$, $B_1$ и $B_2$ — на стороне $AC$, $C_1$ и $C_2$ — на стороне $AB$). Докажите, что если прямая $A_1B_1$ параллельна биссектрисе угла $B$, то прямая $A_2C_2$ параллельна биссектрисе угла $C$. ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №49. В клетках таблицы $11 \times 11$ расставлены все натуральные числа от 1 до 121. Дима посчитал произведение чисел в каждой строке, а Саша — произведение чисел в каждом столбце. Могли ли они получить одинаковые наборы из 11 чисел? ( С. Берлов )
комментарий/решение олимпиада
Задача №50. Точка $I$ — центр вписанной окружности треугольника $ABC$. Окружность, проходящая через вершины $B$ и $C$, пересекает отрезки $BI$ и $CI$ в точках $P$ и $Q$ соответственно. Известно, что $BP\cdot CQ=PI\cdot QI$. Докажите, что описанная окружность треугольника $PQI$ касается описанной окружности исходного треугольника. ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №51. Организаторы математического конгресса обнаружили, что, если любого из участников поселить в одноместный номер, то всех остальных можно будет расселить по двухместным номерам, в каждом из которых обитатели будут знакомы друг с другом.
Докажите, что любой участник может организовать круглый стол по теории графов, в котором, кроме него, будет участвовать еще четное число людей, и каждый участник будет знаком с обоими своими соседями по столу. ( С. Берлов, С. Иванов )
комментарий/решение олимпиада
Задача №52. Точка $H$ — ортоцентр остроугольного треугольника $ABC$. На стороне $BC$ выбрана точка $D$. Точка $P$ построена таким образом, что $ADPH$ — параллелограмм. Докажите, что $\angle BPC > \angle BAC$. ( С. Берлов )
комментарий/решение олимпиада
Задача №53. Саша и Дима играют в игру на доске $100\times 100$. В начале игры Саша выбирает 50 клеток и ставит на них по одному королю. После этого Дима выбирает одну из свободных клеток и выставляет на нее ладью. Далее игроки ходят по очереди (начинает Саша). Каждым своим ходом Саша перемещает каждого из королей на соседнюю по стороне или углу клетку, а Дима своим ходом передвигает ладью на любое количество клеток по горизонтали или вертикали. При этом ладья не может "перепрыгивать" через короля и "бить" короля. Сможет ли Саша действовать так, чтобы рано или поздно побить ладью одним из королей? ( С. Берлов )
комментарий/решение олимпиада
Задача №54. Расстановку фишек в клетках квадрата $n\times n$ назовем редкой, если в любом квадрате $2\times 2$ стоит не более 3 фишек. Сергей поставил в некоторые клетки доски по одной фишке так, что получилась редкая расстановка. Он заметил, однако, что если переставить любую фишку на любую свободную клетку, то перестановка перестанет быть редкой. При каких $n$ это возможно? ( С. Берлов )
комментарий/решение олимпиада
Задача №55. Точка $M$ — середина основания $BC$ трапеции $ABCD$. На основании $AD$ выбрана точка $P$. Прямая $PM$ пересекает прямую $CD$ в точке $Q$, причем $C$ лежит между $Q$ и $D$. Перпендикуляр к основаниям, проведенный через точку $P$, пересекает прямую $BQ$ в точке $K$. Докажите, что $\angle QBC = \angle KDA$. ( С. Берлов )
комментарий/решение(3) олимпиада
Задача №56. 100 клеток бесконечной клетчатой плоскости образуют квадрат $10\times 10$. Единичные отрезки, являющиеся сторонами этих клеток, покрашены в несколько цветов. Оказалось, что на границе любого квадрата со сторонами, идущими по линиям сетки, присутствуют отрезки не более, чем двух цветов. (Рассматриваемые квадраты не обязаны содержаться в исходном квадрате $10\times 10$.) Какое наибольшее количество цветов может присутствовать в раскраске? ( С. Берлов )
комментарий/решение олимпиада
Задача №57. На бесконечной клетчатой плоскости стоит несколько шахматных коней. При этом никакая клетка не находится под боем более, чем одного коня. (В частности, клетка, на которой стоит конь, может биться другим конем, но не двумя сразу). Саша обвел контур прямоугольника $14\times 16$. Какое наибольшее количество коней могло попасть в этот прямоугольник? ( С. Берлов )
комментарий/решение олимпиада
Задача №58. Из картонного клетчатого прямоугольника $8\times 7$ вырезан уголок, состоящий из всех клеток первой строки и первого столбца (всего в нем $14$ клеток). Клетки бесконечной клетчатой плоскости покрашены в $k$ цветов так, что при любом положении картонного уголка на этой плоскости (с учетом поворотов и переворотов) все покрытые им клетки имеют разный цвет. При каком наименьшем $k$ это возможно? ( С. Берлов )
комментарий/решение олимпиада
Задача №59. Организаторы математического конгресса обнаружили, что, если любого из участников поселить в одноместный номер, то всех остальных можно будет расселить по двухместным номерам, в каждом из которых обитатели будут знакомы друг с другом. Докажите, что любой участник может организовать круглый стол по теории графов, в котором, кроме него, будет участвовать еще четное число людей, и каждый участник будет знаком с обоими своими соседями по столу. ( С. Берлов, С. Иванов )
комментарий/решение олимпиада
Задача №60. Точки $X$ и $Y$ — середины сторон $AB$ и $AC$ треугольника $ABC$, $I$ — центр его вписанной окружности, $K$ — точка касания вписанной окружности со стороной $BC$. Биссектриса внешнего угла при вершине $B$ пересекает прямую $XY$ в точке $P$, а биссектриса внешнего угла при вершине $C$ пересекает $XY$ в точке $Q$. Докажите, что площадь четырехугольника $PKQI$ равна половине площади исходного треугольника. ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №61. В треугольнике $ABC$ проведена медиана $BD$. Биссектрисы углов $ABD$ и $ACB$ перпендикулярны. Найдите наибольшее возможное значение угла $BAC$. ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №62. На футбольном поле тренировалось $n$ футболистов — нападающих и вратарей. Всего на тренировке было забито $k$ голов. Докажите, что после тренировки Фабио Капелло может так раздать номера от 1 до $n$ игрокам, что для любого гола разность между номерами нападающего и вратаря была не менее $n-k$. ( С. Берлов )
комментарий/решение олимпиада
Задача №63. Точки $X$ и $Y$ внутри ромба $ABCD$ таковы, что точка $Y$ лежит внутри выпуклого четырёхугольника $BXDC$ и $2\angle XBY=2\angle XDY=\angle ABC$. Докажите, что прямые $AX$ и $CY$ параллельны. ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №64. Внутри треугольника $ABC$ выбрана точка $P$ таким образом, что $\angle PAB=\angle PCB={1\over 4}(\angle A+\angle C)$. $BL$ — биссектриса этого треугольника. Прямая $PL$ пересекает описанную окружность треугольника $APC$ в точке $Q$. Докажите, что прямая $QB$ — биссектриса угла $AQC$. ( С. Берлов )
комментарий/решение олимпиада
Задача №65. Барон Мюнхгаузен хвастается, что знает замечательный квадратный трехчлен с положительными коэффициентами: он сам имеет целый корень; если ко всем его коэффициентам прибавить по единице, то полученный трехчлен снова будет иметь целый корень; если второй раз прибавить ко всем коэффициентам по единице, то и этот трехчлен будет иметь целый корень. Не обманывает ли барон? ( С. Берлов )
комментарий/решение олимпиада
Задача №66. По кругу стоят 2010 цифр, каждая из которых равна 1, 2 или 3. Известно, что при любом $k$ в любом блоке из $3k$ подряд идущих цифр каждая из цифр 1, 2, 3 встречается не больше $k+10$ раз. Докажите, что существует блок из нескольких подряд идущих цифр, в котором цифр каждого из видов поровну. ( С. Берлов )
комментарий/решение олимпиада
Задача №67. Точка $H$ — ортоцентр остроугольного треугольника $ABC$. Внутри стороны $BC$ выбрана точка $D$. Точка $P$ построена таким образом, что $ADPH$ — параллелограмм. Докажите, что $\angle DCP < \angle BHP$. ( С. Берлов )
комментарий/решение олимпиада
Задача №68. Саша и Дима играют в игру на доске $100\times 100$. В начале игры Саша выбирает 50 клеток и ставит на них по одному королю. После этого Дима выбирает одну из свободных клеток и выставляет на нее ладью. Далее игроки ходят по очереди (начинает Саша). Каждым своим ходом Саша перемещает каждого из королей на соседнюю по стороне или углу клетку, а Дима своим ходом передвигает ладью на любое количество клеток по горизонтали или вертикали. При этом ладья не может "перепрыгивать" через короля и "бить" короля. Сможет ли Саша действовать так, чтобы рано или поздно побить ладью одним из королей? ( С. Берлов )
комментарий/решение олимпиада
Задача №69. На стороне $AB$ вписанного четырехугольника $ABCD$ нашлась такая точка $X$, что отрезок $CX$ делится пополам диагональю $BD$, а отрезок $DX$ делится пополам диагональю $AC$. Какое наименьшее значение может принимать величина $AB\over CD$? ( С. Берлов )
комментарий/решение олимпиада
Задача №70. В городе Гамильтоновске каждая улица соединяет две площади, причем с любой площади можно по улицам попасть на любую другую. Губернатор обнаружил, что если закрыть на ремонт все площади произвольного маршрута, который не проходит ни по какой площади дважды, то все равно с любой из оставшихся площадей можно будет попасть на любую другую. Докажите, что существует маршрут, который проходит по каждой площади города ровно по одному разу и заканчивается там же, где начинается. ( С. Берлов )
комментарий/решение олимпиада
Задача №71. На бесконечной клетчатой плоскости стоит несколько шахматных коней. При этом никакая клетка не находится под боем более, чем одного коня. (В частности, клетка, на которой стоит конь, может биться другим конем, но не двумя сразу). Саша обвел контур прямоугольника $14\times 16$. Какое наибольшее количество коней могло попасть в этот прямоугольник? ( С. Берлов )
комментарий/решение олимпиада
Задача №72. Даны два натуральных числа $a < b$. Докажите, что из любых $b$ последовательных натуральных чисел можно выбрать два числа, произведение которых делится на $ab$. ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №73. Из картонного клетчатого прямоугольника $n\times (n-1)$ вырезан уголок, состоящий из всех клеток первой строки и первого столбца (всего в нем $2n-2$ клетки). Клетки бесконечной клетчатой плоскости покрашены в $k$ цветов так, что при любом положении картонного уголка на этой плоскости (с учетом поворотов и переворотов) все покрытые им клетки имеют разный цвет. При каком наименьшем $k$ это возможно? ( С. Берлов )
комментарий/решение олимпиада
Задача №74. Имеется 25 масок, каждая своего цвета. $k$ мудрецов играют в игру: им показывают все маски, потом они договариваются между собой, после чего им надевают маски таким образом, что каждый из них видит маски на всех остальных (но не знает, на ком они надеты) и не видит свою. Никакие формы взаимодействия при этом не разрешаются. Все они одновременно называют по одному цвету, пытаясь угадать цвет своей маски. При каком наименьшем $k$ они могут так заранее договориться, чтобы хотя бы один из них непременно угадал? ( С. Берлов )
комментарий/решение олимпиада
Задача №75. Даны два ненулевых числа. Если к каждому из них прибавить единицу, а также из каждого из них вычесть единицу, то сумма обратных величин четырёх полученных чисел будет равна 0. Какое число может получиться, если из суммы исходных чисел вычесть сумму их обратных величин? Найдите все возможности. ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №76. По кругу сидят 100 человек. Некоторые из них --- рыцари, всегда говорящие правду, остальные --- лжецы, которые всегда лгут. Для некоторого натурального числа $k < 100$ каждый из сидящих произнёс фразу: «Следующие $k$ людей, сидящих за мной по часовой стрелке --- лжецы». Чему могло быть равно число $k$? ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №77. В Тридесятом царстве из каждого города выходит по 30 дорог, причём каждая дорога соединяет два города, не проходя через другие города. Тридесятый царь захотел разместить в некоторых городах по дорожно-эксплуатационному управлению (ДЭУ), обслуживающему все выходящие из города дороги, так, чтобы каждая дорога обслуживалась хотя бы одним управлением и управления были размещены не более чем в половине городов. Может ли так оказаться, что у царя существует ровно 2018 способов сделать это? ( И. Богданов, С. Берлов )
комментарий/решение(1) олимпиада
Задача №78. На клетчатой белой доске размером $25\times25$ клеток несколько клеток окрашено в чёрный цвет, причём в каждой строке и каждом столбце окрашено ровно 9 клеток. При каком наименьшем $k$ заведомо можно перекрасить $k$ клеток в белый цвет таким образом, чтобы нельзя было вырезать чёрный квадрат $2\times2$? ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №79. Диагонали выпуклого четырёхугольника $ABCD$ равны и пересекаются в точке $K$. Внутри треугольников $AKD$ и $BKC$ выбрали точки $P$ и $Q$ соответственно так, что $\angle KAP = \angle KDP = \angle KBQ = \angle KCQ.$ Докажите, что прямая $PQ$ параллельна биссектрисе угла $AKD$. ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №80. Окружность касается стороны $AB$ треугольника $ABC$ в точке $A$, стороны $BC$ — в точке $P$ и пересекает сторону $AC$ в точке $Q$. Прямая, симметричная $PQ$ относительно $AC$, пересекает прямую $AP$ в точке $X$. Докажите, что $PC=CX$. ( С. Берлов )
комментарий/решение(2) олимпиада
Задача №81. На столе лежат 99 одинаковых с виду шаров, 50 из них — медные, и 49 — цинковые. Лаборант пронумеровал шары. За одну проверку на спектрометре можно выяснить, сделаны ли положенные в него два шара одного и того же металла. Но результаты выдаются только на следующий день. За какое минимальное число проверок можно узнать, из какого металла сделал каждый шар, если надо все проверки провести сегодня? ( С. Берлов, Н. Власова )
комментарий/решение(1) олимпиада
Задача №82. Есть 40 гирь. Веса любых двух отличаются не более чем на 45 кг. Любые десять из этих гирь можно разбить на две группы по пять гирь, суммы весов которых отличаются не более чем на 11 кг. Докажите, что найдутся две гири, веса которых отличаются не более чем на 1 кг. ( С. Берлов, Д. Ширяев )
комментарий/решение(1) олимпиада
Задача №83. Дано 1000-значное число без нулей в записи. Докажите, что из этого числа можно вычеркнуть несколько (возможно, ни одной) последних цифр так, чтобы получившееся число не было натуральной степенью числа, меньшего 500. ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №84. Дан выпуклый четырёхугольник $ABSC.$ На диагонали $BC$ выбрана точка $P$ так, что $AP = CP > BP.$ Точка $Q$ симметрична точке $P$ относительно середины диагонали $BC,$ а точка $R$ симметрична точке $Q$ относительно прямой $AC.$ Оказалось, что $\angle SAB = \angle QAC$ и $\angle SBC = \angle BAC.$ Докажите, что $SA = SR.$ ( С. Берлов )
комментарий/решение(2) олимпиада
Задача №85. Окружность $\omega$ касается сторон $AB$ и $BC$ треугольника $ABC$ и пересекает сторону $AC$ в точке $K$. Оказалось, что касательная к $\omega$ в точке $K$ симметрична прямой $AC$ относительно прямой $BK$. Чему может быть равна разность $AK-CK$, если $AB=9$ и $BC=11$? ( С. Берлов )
комментарий/решение олимпиада
Задача №86. Андрей, Боря, Витя и Гена играют на доске $1000\times 1000$. Ходят по очереди — сначала Андрей, потом Боря, затем Витя и наконец Гена, затем снова Андрей и т.д. Каждым ходом игрок должен закрасить еще незакрашенные клетки, образующие прямоугольник $2\times 1$, $1\times 2$, $1\times 3$ или $3\times 1$. Проигрывает тот, кто не может сделать ход. Докажите, что какие-то трое ребят могут договориться и играть так, чтобы оставшийся заведомо проиграл. ( С. Берлов, Н. Власова )
комментарий/решение(1) олимпиада
Задача №87. На окружности отмечено 150 серых, 151 бурая и 152 малиновых точки таким образом, что никакие две одноцветные точки не стоят рядом. Докажите, что найдётся бурая точка, у которой оба соседа — малиновые. ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №88. Имеется 70 переключателей и 15 ламп. Каждая лампа соединена с 35 переключателями. Никакие два переключателя не соединены с одним и тем же набором ламп. Нажатие на переключатель меняет состояние всех ламп, с которыми он соединён (включённые выключает и наоборот). Изначально все лампы выключены. Докажите, что можно нажать на какие-то 19 переключателей таким образом, чтобы включилось не менее восьми ламп. ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №89. На доске написано $n$ целых чисел, любые два из которых отличаются хотя бы на 3. Сумма квадратов двух наибольших из них меньше 500. Сумма квадратов двух наименьших из них также меньше 500. При каком наибольшем $n$ это возможно? ( Р. Женодаров, С. Берлов )
комментарий/решение(1) олимпиада
Задача №90. Биссектриса угла $A$ выпуклого четырёхугольника $ABCD$ пересекает сторону $CD$ в точке $K.$ Оказалось, что $DK = BC$ и $KC+AB = AD.$ Докажите, что $\angle BCD = \angle ADC.$ ( С. Берлов )
комментарий/решение(2) олимпиада
Задача №91. На полуокружности расположено 50 точек. Любые две точки, между которыми не более 9 других точек, соединены отрезком. Степенью точки назовём количество отрезков, выходящих из неё. Панда и Вомбат играют в игру. Ходят по очереди, начинает Панда. Панда своим ходом может стереть один отрезок, соединяющий точки, сумма степеней которых чётна. Вомбат может своим ходом стереть один отрезок, соединяющий точки, сумма степеней которых нечётна. Проигрывает тот, кто не может сделать ход. Кто из зверей выиграет при правильной игре? ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №92. В строку выписано 1999 натуральных чисел. Во вторую строку под каждыми двумя соседними числами выписали их наибольший общий делитель. Аналогичным образом получили третью, четвёртую и т. д. строки. Может ли 1000-я строка состоять из 1000 последовательных чисел в некотором порядке? ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №93. В стране Анчурии провели выборы президента. По всем избирательным участкам была разослана директива, что действующий президент Мирафлорес на каждом участке должен набрать более 95$\%$ голосов. Для этого на всех участках выбрали ближайшее кратное 100 число, большее количества избирателей на этом участке, после чего отсчитали 95$\%$ от этого числа и записали в протокол как проголосовавших за Мирафлореса. После подсчёта по всем участкам оказалось, что Мирафлорес набрал более 100$\%$ голосов. Докажите, что на каком-то участке было менее 2020 избирателей. ( С. Берлов )
комментарий/решение(4) олимпиада
Задача №94. В автобусе ехали мужчины и женщины, всего 32 человека. Каждый из пассажиров знаком ровно с одним мужчиной и ровно с одной женщиной из остальных. $N$ пассажиров одновременно узнали некоторую новость. Далее каждую минуту новость узнавал от кого-то из своих знакомых ещё один пассажир, причём если это была женщина, то новость в этот момент уже знали оба её знакомых. Через несколько минут оказалось, что новость знают все пассажиры. При каком наименьшем $N$ такое могло случиться? ( С. Берлов, Н. Власова )
комментарий/решение(1) олимпиада
Задача №95. $AH$ — высота равнобедренного треугольника $ABC$ $(AB = BC).$ $HK$ — высота треугольника $AHB.$ Оказалось, что $4HK = AB.$ Чему могла быть равна градусная мера угла $ABC?$ Принимаются только ответы, данные в виде целых чисел или десятичных дробей. ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №96. У Васи есть 20 гирь, среди которых нет трёх, равных по весу. Он может разложить эти все гири как на 10, так и на 11 куч с равными весами. Докажите, что у Васи найдутся две гири, веса которых различаются ровно в 4 раза. ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №97. В трапеции $ABCD$ биссектриса угла $B$ пересекает основание $AD$ в точке $L.$ Точка $M$ — середина стороны $CD.$ Прямая, параллельная $BM$ и проходящая через $L,$ пересекает сторону $AB$ в точке $K.$ Оказалось, что угол $BLM$ — прямой. Найдите отношение $BK/KA.$ ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №98. В группе из 79 школьников у каждого не более 39 знакомых, причем у любого мальчика есть знакомая девочка, а у любой девочки — знакомый мальчик. Может ли оказаться, что все девочки из этой группы имеют в ней поровну знакомых мальчиков, а все мальчики — поровну знакомых девочек? Все знакомства — взаимные. ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №99. Петя и Вася играют в игру. Вася кладёт в ряд 150 монет: некоторые «орлом» вверх, некоторые — «решкой». Петя своим ходом может показать на любые три лежащие подряд монеты, после чего Вася обязан перевернуть какие-то две монеты из этих трёх по своему выбору. Петя хочет, чтобы как можно больше монет лежали «решкой» вверх, а Вася хочет ему помешать. При каком наибольшем $k$ Петя сможет независимо от действий Васи добиться того, чтобы хотя бы $k$ монет лежали «решкой» вверх? ( С. Берлов, Н. Власова )
комментарий/решение(1) олимпиада
Задача №100. $CL$ — биссектриса треугольника $ABC.$ $CLBK$ — параллелограмм. Прямая $AK$ пересекает отрезок $CL$ в точке $P.$ Оказалось, что точка $P$ равноудалена от диагоналей параллелограмма $CLBK.$ Докажите, что $AK \ge CL.$ ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №101. Точка $M$ — середина стороны $AC$ равностороннего треугольника $ABC.$ Точки $P$ и $R$ на отрезках $AM$ и $BC$ соответственно выбраны так, что $AP = BR.$ Найдите сумму углов $ARM,$ $PBM$ и $BMR.$ ( С. Берлов )
комментарий/решение(3) олимпиада
Задача №102. Кощей Бессмертный открыл счет в банке «Спёрбанк». Изначально на счете было 0 рублей. В первый день Кощей кладёт на счёт $k$ $(k > 0)$ рублей, а каждый следующий день добавляет туда на один рубль больше, чем накануне (на второй день он добавляет $k+1$ рублей, на третий — $k+2$ рубля и т. д.) Каждый раз сразу после того, как Кощей вносит деньги на счёт, общая величина счёта уменьшается банком в два раза. Найдите все такие $k,$ при которых сумма на счёте всегда будет выражаться целым числом рублей. ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №103. На сторонах $AB$ и $BC$ треугольника $ABC$ выбраны точки $P$ и $Q$ соответственно. Отрезки $CP$ и $AQ$ пересекаются в точке $R.$ Оказалось, что $AR = CR = PR+QR.$ Докажите, что из отрезков $AP,$ $CQ$ и $PQ$ можно составить треугольник, один из углов которого равен углу $B.$ ( С. Берлов )
комментарий/решение(4) олимпиада
Задача №104. При каких натуральных $n$ можно так отметить несколько клеток доски $n\times n$, чтобы во всех строках и столбцах было чётное число отмеченных клеток, а на всех $4n-6$ диагоналях, длина которых больше одной клетки, — нечётное? ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №105. Петя, Вася и Толя вернулись с рыбалки, на которой каждый из них поймал некоторое количество рыб (хотя бы одну). После рыбалки они стали хвастаться своими уловами. Петя сказал: «Я поймал рыб не меньше, чем каждый из остальных!». Вася сказал: «Я поймал рыб не меньше, чем Петя и Толя в сумме!». Толя сказал: «Я поймал на $25\%$ больше рыб, чем Вася!». Позже выяснилось, что каждый из ребят преувеличил свой улов не более, чем в $a$ раз. Какое наименьшее значение могло принимать число $a$? ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №106. Дано натуральное число $n.$ За одну операцию можно либо вычесть из имеющегося числа любое натуральное число, меньшее его наименьшего простого делителя, либо разделить его на его наименьший простой делитель. Существует ли такое составное $n,$ что из него нельзя получить простое число менее, чем за 2021 операцию? ( С. Берлов )
комментарий/решение(2) олимпиада
Задача №107. На доске написано четыре положительных числа. Докажите, что какие-то два из них отличаются меньше, чем на треть суммы двух остальных. ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №108. В лагерь приехали 99 школьников, причём все приехавшие имеют одно и то же ненулевое количество знакомых среди остальных. Группу ребят, обладающую тем свойством, что любой из приехавших, не входящий в эту группу, знаком с кем-то из этой группы, будем называть популярной. Докажите, что из любой популярной группы, содержащей более 49 ребят, можно выбрать популярную группу, содержащую ровно 49 ребят. ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №109. На каждой стороне выпуклого 100-угольника отметили по две точки, делящие эту сторону на три равные части. После этого всё, кроме отмеченных точек, стерли. Докажите, что по отмеченным точкам можно однозначно восстановить исходный 100-угольник. ( С. Берлов )
комментарий/решение олимпиада
Задача №110. Синусы трех острых углов образуют арифметическую прогрессию, а их косинусы — геометрическую. Докажите, что все три угла равны. ( С. Берлов )
комментарий/решение(3) олимпиада
Задача №111. Дано $n$ различных натуральных чисел. Рассмотрим все $n(n - 1)/2$ попарных сумм этих чисел. Для каждой из этих попарных сумм на доску выписали количество исходных чисел, меньших этой суммы, на которые эта сумма делится. Какое наибольшее значение может принимать сумма выписанных на доске чисел? ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №112. В деревне некоторые пары домов соединены дорогами. Жильцы домов, соединённых дорогой, называются соседями. Всегда ли в каждый из этих домов можно поселить рыцаря, который всегда говорит правду, либо лжеца, который всегда лжёт, чтобы каждый житель смог сказать фразу «среди моих соседей лжецов хотя бы вдвое больше, чем рыцарей»? ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №113. Стороны 100 одинаковых равносторонних треугольников покрашены в 150 цветов так, что в каждый цвет покрашены ровно две стороны. Если приложить два треугольника одноцветными сторонами, то полученный ромб будем называть хорошим. Петя хочет сложить из этих треугольников как можно больше хороших ромбов, причем каждый треугольник должен входить не более, чем в один ромб. Какое наибольшее количество хороших ромбов может гарантировать себе Петя независимо от способа раскраски треугольников? ( И. Рубанов, С. Берлов )
комментарий/решение(1) олимпиада
Задача №114. Можно ли отметить несколько клеток в таблице $9 \times 9,$ чтобы в любых двух соседних строках таблицы было отмечено не меньше 6 клеток, а в любых двух соседних столбцах — не больше 5 клеток? ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №115. Петя и Вася написали на доске по 100 различных натуральных чисел. Петя поделил все свои числа на Васины с остатком и выписал все 10000 получившихся остатков себе в тетрадь. Вася поделил все свои числа на Петины с остатком и выписал все 10000 получившихся остатков себе в тетрадь. Оказалось, что наборы выписанных Васей и Петей остатков совпадают. Докажите, что тогда и наборы их исходных чисел совпадают. ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №116. Натуральные числа $a$, $b$ и $c$, большие 2022, таковы, что $a+b$ делится на $c-2022$, $a+c$ делится на $b-2022$, $b+c$ делится на $a-2022$. Какое наибольшее значение может принимать число $a+b+c$? ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №117. В выпуклом пятиугольнике $ABCDE$ диагонали $AD$ и $CE$ пересекаются в точке $X$. Оказалось, что $ABCX$ — параллелограмм и $BD = CX;$ $BE = AX.$ Докажите, что $AE = CD.$ ( С. Берлов )
комментарий/решение(2) олимпиада
Задача №118. Докажите, что для любого целого неотрицательного числа $k$, не превосходящего $\frac{2022\cdot 2021}{2},$ существуют такие 2022 числа, что все их $\frac{2022\cdot 2021}{2}$ попарные суммы различны и среди этих сумм ровно $k$ положительных. (И. Рубанов, С. Берлов, Л. Самойлов) ( И. Рубанов, С. Берлов, Л. Самойлов )
комментарий/решение(1) олимпиада
Задача №119. За круглым столом сидели 99 человек, все разного роста. Каждый честно ответил на два вопроса:
1. <<Вы выше, чем ваш сосед справа?>>
2. <<Вы выше, чем оба ваших соседа — справа и слева?>>.
Какое наибольшее количество ответов <<Да>> могло быть дано? ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №120. Запишите четыре числа (не обязательно целых), среди которых нет одинаковых, чтобы выполнялось такое условие: если число $x$ есть среди записанных, то хотя бы одно из чисел $x-1$ или $6x-1$ тоже есть среди записанных. ( И. Рубанов, С. Берлов )
комментарий/решение(2) олимпиада
Задача №121. Делители натурального числа $n$ (включая $n$ и 1), имеющего больше трёх делителей, выписали по возрастанию: $1 = d_1 < d_2 < \ldots < d_k = n$. Разности $u_1 = d_2-d_1$, $u_2 = d_3-d_2$, $\ldots$, $u_{k-1} = d_k-d_{k-1}$ оказались такими, что $u_2-u_1 = u_3-u_2 = \ldots = u_{k-1}-u_{k-2}$. Найдите все такие $n$. ( С. Берлов )
комментарий/решение(3) олимпиада
Задача №122. $BM$ — медиана остроугольного треугольника $ABC$. Биссектриса угла $C$ пересекает прямую, проходящую через $A$ параллельно $BC$, в точке $X$. Оказалось, что $BM = MX$. Докажите, что $BC > AC$. ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №123. На доске написаны натуральные числа от 1 до 1000, по одному разу каждое. Вася может стереть любые два числа и записать вместо них одно: их наибольший общий делитель или их наименьшее общее кратное. Через 999 таких операций на доске осталось одно число, равное натуральной степени десятки. Какое наибольшее значение она может принимать? ( С. Берлов )
комментарий/решение(2) олимпиада
Задача №124. Точка $N$ — середина стороны $AD$ выпуклого четырёхугольника $ABCD$, а точка $M$ на стороне $AB$ такова, что $CM \perp BD$. Докажите, что если $BM > MA$, то $2BC+AD > 2CN$. ( С. Берлов )
комментарий/решение(4) олимпиада
Задача №125. Дано натуральное число $k$, большее 1. Натуральное число $n$, большее 1 и взаимно простое с $k$, назовём правильным, если для любого натурального делителя $d$ ($d < n$) числа $n$ число ${d+k}$ не взаимно просто с $n$. Докажите, что правильных чисел — конечное количество. ( С. Берлов )
комментарий/решение(2) олимпиада
Задача №126. На стороне $AC$ треугольника $ABC$ выбрана точка $E.$ Биссектриса $AL$ пересекает отрезок $BE$ в точке $X.$ Оказалось, что $AX=XE$ и $AL=BX.$ Чему равно отношение углов $A$ и $B$ треугольника? ( С. Берлов )
комментарий/решение(3) олимпиада
Задача №127. По кругу расставлено 99 положительных чисел. Оказалось, что для любых четырех стоящих подряд чисел сумма двух первых из них по часовой стрелке равна произведению двух последних из них по часовой стрелке. Чему может быть равна сумма всех 99 расставленных чисел? ( С. Берлов )
комментарий/решение(3) олимпиада
Задача №128. Назовем два числа почти равными друг другу, если они равны друг другу или отличаются друг от друга не более, чем на единицу. Клетчатый прямоугольник со сторонами, равными натуральным числам $a$ и $b,$ таков, что из него нельзя по линиям сетки вырезать прямоугольник, площадь которого почти равна половине площади исходного прямоугольника. Какое наименьшее значение может принимать число $|a-b|$? ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №129. Назовем пару различных натуральных чисел хорошей, если одно из них делится на другое. Найдите такие 20 натуральных чисел, среди которых нет равных, что если выписать все возможные пары этих чисел, то количество хороших среди них будет равно 101. (Каждая пара записывается один раз. Порядок чисел в парах не учитывается, то есть пары ${(a, b)}$ и ${(b, a)}$ считаются за одну.)
Не забудьте объяснить, почему найденные вами числа действительно дают ровно 101 хорошую пару, не больше и не меньше. Ответы без объяснения не засчитываются. ( И. Рубанов, С. Берлов )
комментарий/решение олимпиада
Задача №130. В равнобедренном треугольнике $ABC$ $(AB = BC)$ точка $M$ — середина стороны $AB$, а точка $K$ на стороне $AC$ такова, что $\angle ABK = \angle BKA$. Оказалось, что $KB = KM$. Докажите, что $2AC = 3AB$. ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №131. На доске написано 100 чисел. Оказалось, что произведение любых двух написанных чисел равно сумме всех остальных. Чему может быть равна сумма всех написанных чисел? ( С. Берлов )
комментарий/решение(3) олимпиада
Задача №132. Существует ли такое нечетное натуральное число $n$, что неполные частные от деления $n$ на все натуральные числа от 10 до 1000 включительно — это различные нечетные простые числа, а остатки — составные числа (не обязательно различные)? Напомним, что 0 не является составным числом. ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №133. В белой таблице размером $100\times 100$ клеток окрашено в красный цвет $N$ ($N > 0$) клеток таким образом, что количество красных клеток в любой фигуре, образованной объединением столбца и строки таблицы, делится на 3. Чему может быть равно $N$? ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №134. В каждой клетке шахматной доски стоит нуль. Петя и Вася играют в игру. Ходят по очереди, начинает Петя. Петя каждым своим ходом выбирает какой-то квадрат из четырех клеток и к каждому из чисел, стоящих в этом квадрате, прибавляет нуль или единицу, по своему выбору (выбор для каждой из четырех клеток совершается отдельно, то есть может случиться, что в некоторых клетках прибавляется нуль, а в некоторых — единица). Вася своим ходом выбирает какую-то клетку и прибавляет к стоящему в ней числу нуль или единицу, по своему выбору. Петя хочет, чтобы после 2024-го хода (т. е., после того как он и Вася сделают по 1012 ходов) на доске было как можно больше нечетных чисел. Какое наибольшее количество нечетных чисел он может получить независимо от действий Васи? ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №135. Целые числа $x$, $y$, $z$, $t$ таковы, что $x+y+z+t = 0$. Сколько различных натуральных значений, не превосходящих 10000, может принимать число $(xy-zt)(xz-yt)(yz-xt)?$ ( С. Берлов, Л. Самойлов )
комментарий/решение(1) олимпиада
Задача №136. В трапеции $ABCD$ диагональ $BD$ является биссектрисой угла $ADC$. На основаниях $BC$ и $AD$ выбрали точки $X$ и $Y$ соответственно таким образом, что $AX = BD$ и $AY = CD$. Оказалось, что $\angle BCD = 130^\circ$. Найдите величину угла $AXY$. ( С. Берлов )
комментарий/решение(11) олимпиада
Задача №137. В выпуклом пятиугольнике $ABCDE$ $\angle ACB=\angle CBD=\angle DCE=\angle BDC=30^\circ$, а $AB+BC+CD+DE=AD+BE$. Чему может быть равен угол $A$ этого пятиугольника? ( С. Берлов )
комментарий/решение(1) олимпиада
Задача №138. На плоскости даны точки $A$ и $B$, а также прямая $\ell$, не перпендикулярная $A B$ и не пересекающая отрезок $A B$. Рассматриваются всевозможные окружности с центрами $O \notin \ell$, проходящие через точки $A$ и $B$ и пересекающие $\ell$ в двух точках — обозначим эти точки $C$ и $D$. Докажите, что все описанные окружности треугольников $O C D$ касаются одной и той же фиксированной окружности. ( С. Берлов )
комментарий/решение олимпиада
Задача №139. На 2025 досках написали по натуральному числу. Разрешается проделывать такую операцию: на одной из досок вместо написанного на ней числа записать его куб, а на каждой из остальных досок вместо написанного на ней числа записать в три раза меньшее число, если оно является целым (если хотя бы одно из чисел после деления на 3 становится нецелым, операция невозможна!). Можно ли написать такие числа и проделать несколько (не меньше одной) операций так, чтобы после последней операции на каждой доске оказалось исходное число? ( С. Берлов, А. Голованов )
комментарий/решение(1) олимпиада
Задача №140. Из доски $100\times 100$ вырезаны 4 угловых клетки. Какое наименьшее количество клеток надо ещё вырезать, чтобы из оставшейся части нельзя было бы вырезать квадрат $2\times 2$? ( С. Берлов )
комментарий/решение олимпиада
Задача №141. В вершины правильного 100-угольника поставили 100 фишек, на которых написаны номера 1, 2, $\ldots,$ 100, именно в таком порядке по часовой стрелке. За ход разрешается обменять местами некоторые две фишки, стоящие в соседних вершинах, если номера этих фишек отличаются не более чем на k. При каком наименьшем k серией таких ходов можно добиться расположения, в котором каждая фишка сдвинута на одну позицию по часовой стрелке по отношению к своему начальному положению? ( С. Берлов )
комментарий/решение(1) олимпиада
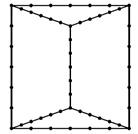
Задача №142. На рисунке изображён автодром; точки — это перекрёстки, отрезки — дороги. Каждый отрезок между соседними точками машина проезжает ровно за минуту. Приехав на перекрёсток, машина немедленно уезжает с него по любой дороге, кроме той, по которой она приехала. Сначала несколько машин расположены на перекрёстках, затем они одновременно начинают двигаться по указанным правилам. При каком наибольшем количестве машин может случиться, что они смогут неограниченно долго ездить, никогда не встречаясь (ни на перекрёстках, ни на дорогах)?
комментарий/решение олимпиада