Олимпиада имени Леонарда Эйлера 2018-2019 учебный год, I тур заключительного этапа

Дан выпуклый четырёхугольник $ABSC.$ На диагонали $BC$ выбрана точка $P$ так, что $AP = CP > BP.$ Точка $Q$ симметрична точке $P$ относительно середины диагонали $BC,$ а точка $R$ симметрична точке $Q$ относительно прямой $AC.$ Оказалось, что $\angle SAB = \angle QAC$ и $\angle SBC = \angle BAC.$ Докажите, что $SA = SR.$ ( С. Берлов )

Комментарий/решение

Комментарии от администратора Комментарии от администратора №1.     Отметим на отрезке $AC$ такую точку $L,$ что $QL \parallel AP.$ Тогда треугольники $APC$ и $LQC$ подобны и $LQ = QC = BP.$ Кроме того, $BQ = PC = AP$ и $\angle APB = \angle LQB,$ поэтому треугольники $ABP$ и $BLQ$ равны по двум сторонам и углу между ними. Следовательно, $BA = BL.$ Далее, $\angle ALR = \angle ALQ = 180^\circ -\angle CLQ = 180^\circ-\angle ACB = \angle CAB+\angle ABC = \angle ABC+\angle SBC = \angle ABS$ и $\angle BAS = \angle QAC = \angle LAR,$ поэтому треугольники $ABS$ и $ALR$ подобны по двум углам, откуда $AB/AL = AS/AR.$ Значит, треугольники $ABL$ и $ASR$ подобны по двум пропорциональным сторонам и углу между ними ($\angle SAR = \angle BAC,$ поскольку $\angle SAB = \angle QAC = \angle RAL$), но так как $AB = BL$, то $AS = SR$.

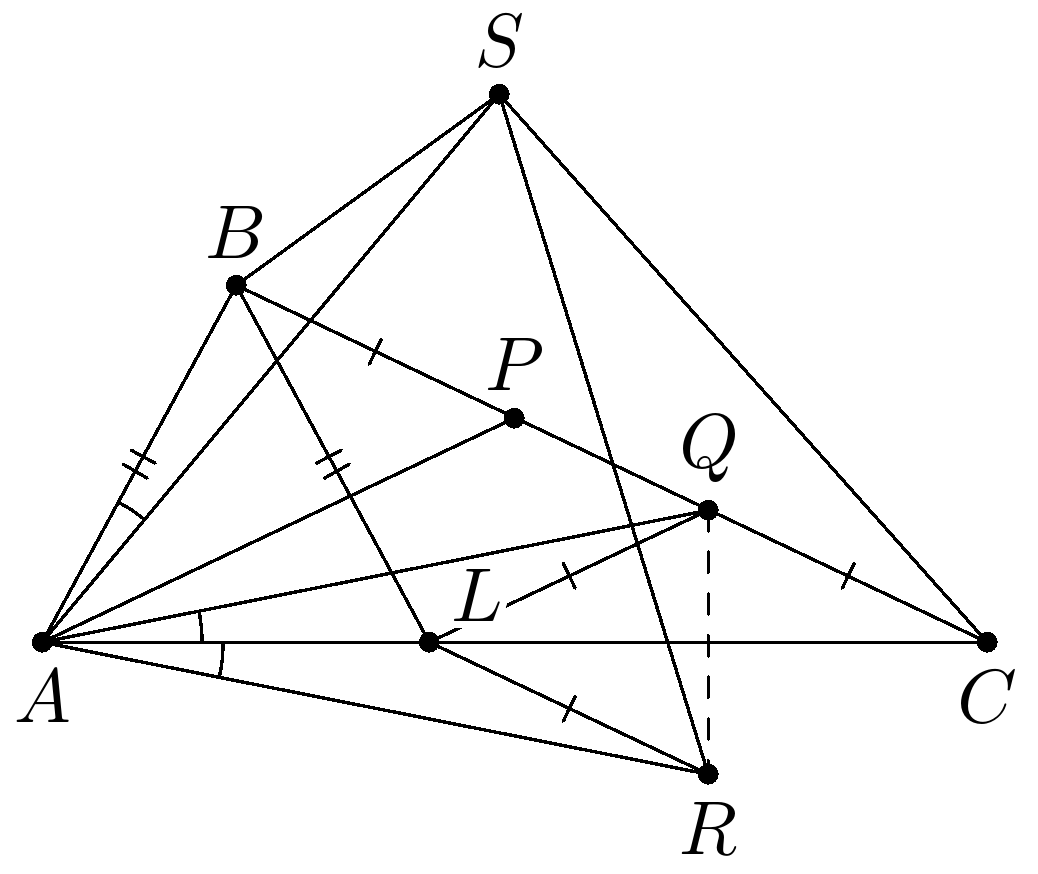
Пусть $AB=c, BC=a, CA=b, \angle ABC=\beta, \angle BCA= \gamma, \angle CAB=\alpha, \angle BAS=x.$

Заметим, что

$$\angle SAR=\angle SAC+\angle CAR=\angle SAC+\angle CAQ=\angle SAC + \angle BAS=\angle BAC=α,$$

поэтому достаточно доказать, что

$$\dfrac {AR}{AS}=2\cos α.$$

По теореме синусов для $\triangle ABS$ , $\triangle AQC$ и $\triangle APQ$

$$\frac{AS}{\sin\angle ABS}=\frac{AB}{\sin\angle ASB}$$

$$\frac{AQ}{\sin\angle ACQ}=\frac{AC}{\sin\angle AQC}$$

$$\frac{AP}{PQ}=\frac{\sin\angle AQP}{\sin\angle PAQ}$$

Легко понять, что

$$\angle ABS=β+α=180-γ,\angle ASB=γ-x,$$

$$\angle ACQ=γ,\angle AQC=180-(γ+x),$$

$$\angle PAQ=γ-x,\angle AQP=\gamma+x.$$

Из симметрии точек $Q$ и $R$ относительно $AC$ получаем, что $AQ=AR$

$$\implies\frac{AS}{AR}=\frac{AS}{AQ}=\frac{AS}{\sin 180-γ}×\frac{sin γ}{AQ}=\frac{AB}{\sin γ-x}×\frac{\sin γ+x}{AC}=$$

$$=\frac{AB}{AC}×\frac{\sin\angle AQP}{\sin\angle PAQ}=\frac{AB}{AC}×\frac{AP}{PQ}=\frac{AB}{PQ}×\frac{AP}{AC}=\frac{c}{PQ}×\frac{\sin γ}{\sin 2γ}.$$

Последнее равенство следует из теоремы Синусов для $\triangle APC.$

Тогда достаточно доказать, что $$2\cos α=\frac{PQ}{c}×\frac{\sin 2γ}{\sin γ}$$ $$\iff$$ $$c\cos α={PQ}×\cos γ$$

Заметим, что $$PQ=PC-QC=PC-BP=PC-(BC-PQ)=2PC-BC=\dfrac{AC}{\cos γ}-BC=\dfrac{b}{\cos γ}-a$$

Значит $$PQ×cos γ=b-a\cos γ=(a\cos γ +c\cos α)-a\cos γ=c\cos α$$ откуда следует требуемое.