Олимпиада имени Леонарда Эйлера2012-2013 учебный год, I тур заключительного этапа

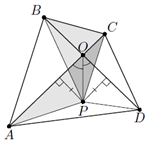
Диагонали выпуклого четырёхугольника $ABCD$ равны и пересекаются в точке $O$. Точка $P$ внутри треугольника $AOD$ такова, что $CD \parallel BP$ и $AB \parallel CP$. Докажите, что точка $P$ лежит на биссектрисе угла $AOD$. ( С. Берлов )

Комментарий/решение

Комментарии от администратора Комментарии от администратора №1.     Решение. Поскольку $AB \parallel CP$, площади треугольников $APC$ и $BPC$ равны. Поскольку $CD \parallel BP$, площади треугольников $BPC$ и $BPD$ равны. Следовательно, площади треугольников $APC$ и $BPD$ равны. Так как $AC = BD$, равны и высоты этих треугольников, опущенные на стороны $AC$ и $BD$ соответственно. Но это означает, что точка $P$, лежащая внутри угла $AOD$, равноудалена от его сторон, и потому лежит на его биссектрисе, что и требовалось доказать.