Ильясов С.
Есеп №1. $X$ және $Y$ нүктелерінде қиылысатын $\omega_1$ және $\omega_2$ шеңберлері $\Omega$ шеңберінің ішінде орналасқан, және оны $A$ және $B$ нүктелерінде жанайды. $AB$ түзуі екінші рет $\omega_1$ және $\omega_2$ шеңберлерін сәйкесінше $A_1$ және $B_1$ нүктерелінде қисын. $A_1B_1X$ қисықсызықты үшбұрышына іштей сызылған шеңбер $A_1B_1$ қабырғасын $Z$ нүктесінде жанасын. $\angle AXZ = \angle BXZ$ теңдігін көрсетіңіз.
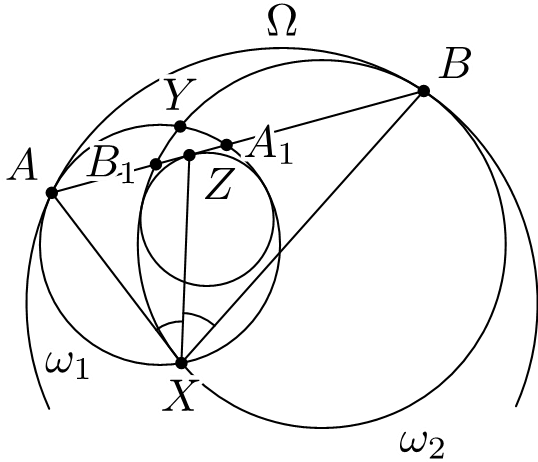
комментарий/решение(2) олимпиада
Есеп №2. Тор $n \times n$ тақтасын (бұл жерде $n \geq 2$) үш бірлік шаршыдан құралған бұрыштармен келесі шарттар орындалатындай жабамыз (бұрышты шексіз рет $90{}^\circ $-қа бұрса болады):
1) тақтаның кез келген шаршысы кемінде бір бұрышпен жабылған.
2) бір бұрышпен жабылып тұрған ортақ қабырғасы бар екі шаршы, бір уақытта одан басқа шаршымен жабылмаған.
Тақтаны ең көп дегенде қанша шаршымен жабуға болады? ( Ильясов С. )
комментарий/решение(3) олимпиада
Есеп №3. $(n+1)(n+2) \dots (n+k)-k$ саны толық квадрат болатындай барлық $(n,k)$ натурал сандар жұптарын табыңыздар. ( Ильясов С., Овчинников Д. )
комментарий/решение(4) олимпиада
Есеп №4. Жазықтықта ешбір үшеуі бір түзудің бойында жатпайтындай және ешбір төртеуі бір шеңбердің бойында жатпайтындай 2015 нүктелер жиыны берілген. Берілген жиындағы қандай да бір үш нүкте арқылы өтетін және қалған нүктелерді қақ бөлетін шеңберлерді қарастырайық (яғни 1006-сы шеңбер ішінде, ал қалған 1006-сы шеңбер сыртында болатын). Осы қарастырып отырған шеңберлер ішінде берілген жиындағы екі нүктеде қиылысатын үш шеңбер табылатынын дәлелдеңіз. ( Ильясов С. )
комментарий/решение олимпиада
Есеп №5. Жазықтықта ешбір үшеуі бір түзудің бойында жатпайтындай және ешбір төртеуі бір шеңбердің бойында жатпайтындай 2015 нүктелер жиыны берілген. Берілген жиындағы қандай да бір үш нүкте арқылы өтетін және қалған нүктелерді қақ бөлетін шеңберлерді қарастырайық (яғни 1006-сы шеңбер ішінде, ал қалған 1006-сы шеңбер сыртында болатын). Осы қарастырып отырған шеңберлер ішінде берілген жиындағы екі нүктеде қиылысатын үш шеңбер табылатынын дәлелдеңіз. ( Ильясов С. )
комментарий/решение(1) олимпиада
Есеп №6. $(n+1)(n+2) \dots (n+k)-k$ саны толық квадрат болатындай барлық $(n,k)$ натурал сандар жұптарын табыңыздар. ( Ильясов С., Овчинников Д. )
комментарий/решение(6) олимпиада
Есеп №7. $ABC$ үшбұрышы $\Gamma$ шеңберіне іштей сызылған. Үшбұрышқа іштей сызылған шеңбер $BC$ қабырғасын $N$ нүктеде жанайды. $\omega $ — $N$ арқылы өтетін және $\Gamma$ шеңберінің $BAC$ сегментіне іштей сызылған шеңбер болсын. $O$ мен $J$ нүктелері сәйкесінше $\omega $ мен $ABC$-ның $BC$ қабырғасын жанайтын іштейсырт сызылған шеңбер центрлері болсын. $AO$ мен $JN$ түзулері параллель екенін дәлелдеңдер. ( Ильясов С. )
комментарий/решение(5) олимпиада
Есеп №8. $O$ нүктесі — сүйірбұрышты $ABC$ үшбұрышына сырттай сызылған шеңбер центрі болсын. $BAC$ бұрышына іштей сызылған және келесі шарттарды қанағаттандыратын $\omega$ және $\Omega$ шеңберлерін қарастырайық: $\omega$ шеңбері $BOC$ үшбұрышына сырттай сызылған шеңбердің $BOC$ доғасын сырттай, ал $\Omega$ шеңбері $ABC$ үшбұрышына сырттай сызылған шеңберді іштей жанайды. $\Omega$ шеңберінің радиусы $\omega$ шеңберінің радиусынан екі есе үлкен екенін дәлелдеңіздер. ( Ильясов С. )
комментарий/решение(1) олимпиада
Есеп №9. Әр тиын, калған басқа тиындарға қарағанда, бір уақытта төмен және оң жағында болмайтындай етіп, өлшемі $n\times n$ болатын тақтаның шаршыларында (тақтаның әр шаршысында бірден көп емес) ең көп дегенде қанша тиын қоюға болады? ( Ильясов С. )
комментарий/решение(1) олимпиада
Есеп №10. Бірінші оқушы $1$, $2$, $\ldots$, $2015$ сандарын шеңбер бойымен қойып шығып, өз дәптеріне көрші тұрған сандардың теріс емес айырмаларын жазып шықты. Екінші оқушы осы сандардан ең кішісін таңдап алу керек. Ол таңдап алған санның ең үлкен мәні неге тең болуы мүмкін? ( Ильясов С. )
комментарий/решение(1) олимпиада
Есеп №11. Сүйірбұрышты $ABC$ үшбұрышының $AA_1$ және $CC_1$ биіктіктері $H$ нүктесінде қиылысады. $AA_1$ биіктігінен $A_1P=AH$ болатындай $P$, ал $CC_1$ биіктігінен $C_1Q=CH$ болатындай $Q$ нүктесі белгіленген. $P$ және $Q$ нүктелерінен сәйкесінше $AA_1$ және $CC_1$ түзулеріне түсірілген перпендикулярлар $ABC$ үшбұрышына сырттай сызылған шеңбер бойында қиылысатынын дәлелдеңіздер. ( Ильясов С. )
комментарий/решение(1) олимпиада
Есеп №12. Әр $i =1, 2, \ldots, 100$ үшін $1 \le x_i \le 2017$ теңсіздігі орындалатын $(x_1,x_2, \ldots,x_{100})$ барлық мүмкін натурал сандар жиынтықтарын қарастырайық. Егер барлық $i =1, 2, \ldots, 100$ үшін $y_i > z_i$ болса, онда $(y_1,y_2, \ldots,y_{100})$ жиынтығын $(z_1,z_2, \ldots,z_{100})$ жиынтығынан үлкен деп айтамыз. Ешқандай жиынтық басқа ешқандай жиынтықтан үлкен болмайтындай, тақтаға ең көп дегенде қанша жиынтықтарды жазып шығуға болады? ( Ильясов С., Аманкельды А. )
комментарий/решение(1) олимпиада
Есеп №13. Кез келген бүтін $x$ және $y$ сандары үшін $f\left( x-f\left( y \right) \right)-f\left( 2x-f\left( y \right) \right)=f{{\left( x \right)}^{2}}$ теңдігі орындалатындай $f:\mathbb{Z}\to \mathbb{Z}$ функциясы берілген. Кез келген бүтін $x$ саны үшін $f\left( f\left( x \right) \right)=0$ теңдігі орындалатынын көрсетіңіз. Бұл жерде $\mathbb{Z}$ — бүтін сандар жиыны. ( Ильясов С. )
комментарий/решение(2) олимпиада
Есеп №14. $М$ – дөңес $n$ бұрышты көпбұрышы берілген. Төбелері $M$-ң төбелерінде болатын кез-келген бесбұрыштың ішінде белгіленген дәл 3 нүкте жататындай етіп, $M$-ң ішіне белгілеуге болатын нүктелердің ең аз саны $k$ болсын. $ k \geq n-2$ болатынын дәлелдеңіз. ( Ильясов С. )
комментарий/решение(4) олимпиада
Есеп №15. Келесі шарттарды қанағаттандыратын барлық $f:\mathbb{N}\rightarrow\mathbb{N}$ функцияларын табыңыз:
(а) кез-келген $k\in S$ үшін, $f\left(k\right)\in S$ болатындай шексіз көп әртүрлі ақырлы $S$ жиындары табылады;
(b) кез-келген әртүрлі $m,n\in\mathbb{N}$ үшін $m-n\ \ |\ \ f\left(m\right)-f(n).$
(«|» бөледі дегенді білдіреді; басқаша айтқанда: $a|b$ болса, онда $b$ саны $a$-ға бөлінеді) ( Ильясов С. )
комментарий/решение(1) олимпиада
Есеп №16. В правильном $n$-угольнике ($n\ge4$) каждая диагональ красится в один из двух цветов. Затем в каждой паре одноцветных пересекающихся диагоналей удаляют одну из этих диагоналей. Какое наибольшее число диагоналей могло остаться при таких операциях? (Диагонали, выходящие из одной вершины, пересекающимися не считаются.) ( Ильясов С. )
комментарий/решение(7) олимпиада
Есеп №17. Множество $\Phi$ состоит из конечного числа точек на плоскости. Расстояние между любыми двумя точками из $\Phi$ по крайней мере $\sqrt{2}$. Известно, что вырезанным из бумаги правильным треугольником со стороной $3$ можно накрыть все точки множества $\Phi$. Из какого наибольшего количества точек может состоять $\Phi$? ( Ильясов С. )
комментарий/решение(1) олимпиада
Есеп №18. Пусть $\mathbb{Q}$ — множество всех рациональных чисел. Найдите все функции $f:\mathbb{Q}\rightarrow \mathbb{Q}$ такие, что для любых $x, y\in\mathbb{Q}$ выполнено равенство $f(x+y)-f(y)=f(f(x-y)+f(y)).$ ( Ильясов С. )
комментарий/решение(5) олимпиада
Есеп №19. Множество $\Phi$ состоит из конечного числа точек на плоскости. Расстояние между любыми двумя точками из $\Phi$ по крайней мере $\sqrt{2}$. Известно, что вырезанным из бумаги правильным треугольником со стороной $3$ можно накрыть все точки множества $\Phi$. Из какого наибольшего количества точек может состоять $\Phi$? ( Ильясов С. )
комментарий/решение(12) олимпиада
Есеп №20. Касательная прямая $l$ к описанной окружности остроугольного треугольника $ABC$ пересекает прямые $AB$, $BC$ и $CA$ в точках $C'$, $A'$ и $B'$ соответственно. Пусть $H$ ---ортоцентр треугольника $ABC$. На прямых $A'H$, $B'H$ и $C'H$ соответственно отмечены точки $A_1$, $B_1$ и $C_1$ (отличные от $H$) такие, что $AH=AA_1$, $BH=BB_1$ и $CH=CC_1$. Доказать, что окружности, описанные около треугольников $ABC$ и $A_1B_1C_1$, касаются. ( Ильясов С. )
комментарий/решение(1) олимпиада
Есеп №21. $ABC$ үшбұрышына іштей сызылған шеңбер $AB, BC, CA$ қабырғаларын сәйкесінше $C_0, A_0, B_0$ нүктелерінде жанайды. $M$ нүктесі — $C_0$ нүктесін $A_0B_0C_0$ үшбұрышының биіктіктер қиылысу нүктесімен қосатын кесіндінің ортасы, ал $N$ нүктесі — $ABC$ үшбұрышына сырттай сызылған шеңбердің $ACB$ доғасының ортасы. $MN$ түзуінің $ABC$-ға іштей сызылған шеңбердің центрі арқылы өтетінін дәлелдеңіз. ( Ильясов С. )
комментарий/решение(8) олимпиада