Республиканская олимпиада по математике, 2016 год, 11 класс
Задача №1. Для любого натурального числа докажите, что все его натуральные делители можно расставить по кругу так, чтобы из любых двух соседних чисел одно число делилось на другое.
(
Д. Елиусизов
)
комментарий/решение(1)
комментарий/решение(1)
Задача №2. Найдите все рациональные числа $a$, для которых существует бесконечно много таких положительных рациональных чисел $q$, что уравнение $\left[ {{x}^{a}} \right]\cdot \left\{ {{x}^{a}} \right\}=q$ не имеет решений в рациональных числах $x$.
(
А. Васильев
)
комментарий/решение(2)
комментарий/решение(2)
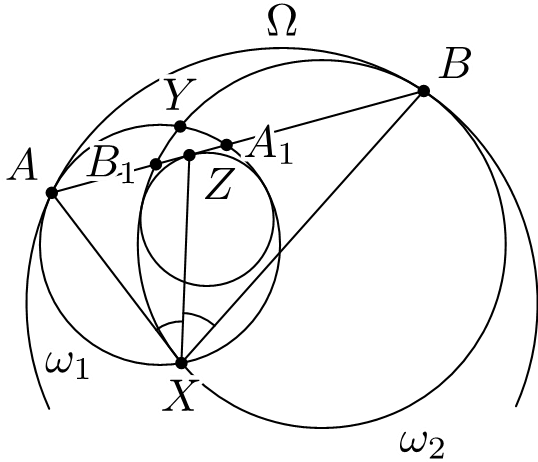
Задача №3. Две пересекающиеся в точках $X$ и $Y$ окружности $\omega_1$ и $\omega_2$ находятся внутри окружности $\Omega$ и касаются ее в точках $A$ и $B$. Прямая $AB$ повторно пересекает окружности $\omega_1$ и $\omega_2$ в точках $A_1$ и $B_1$, соответственно. Вписанная в криволинейный треугольник $A_1B_1X$ окружность касается стороны $A_1B_1$ в точке $Z$. Докажите, что $\angle AXZ=\angle BXZ$.
комментарий/решение(2)
комментарий/решение(2)
Задача №4. В равнобедренном треугольнике $ABC$ точка $H$ — середина основания $AB$, $M$ — середина отрезка $BH$. Пусть $HK$ — высота треугольника $ACH$, а прямые $CM$ и $BK$ пересекаются в точке $L$. Перпендикуляр к прямой $BC$ в точке $B$ и прямая $LH$ пересекаются в точке $N$. Докажите, что угол $BCN$ в два раза меньше угла $ACB.$
(
М. Кунгожин
)
комментарий/решение(2)
комментарий/решение(2)
Задача №5. На плоскости выбраны 101 синяя и 101 красная точка, причем никакие три не лежат на одной прямой. Сумма попарных расстояний между красными точками равна 1 (то есть сумма длин отрезков с концами в красных точках), сумма попарных расстояний между синими тоже равна 1, а сумма длин отрезков с концами разных цветов равна 400. Докажите, что можно провести прямую, отделяющую все красные точки от всех синих.
(
Ким А.
)
комментарий/решение(1)
комментарий/решение(1)
Задача №6. Бесконечная строго возрастающая последовательность $\{a_n\}$ положительных чисел удовлетворяет соотношению
$$a_{n+2}=(a_{n+1}-a_n)^{\sqrt{n}}+n^{-\sqrt{n}}$$
для каждого натурального $n$. Докажите, что для любого $C>0$ существует такое натуральное $m(C)$ (зависящее от $C$), что $a_{m(C)}>C$.
(
Сатылханов К.
)
комментарий/решение(1)
комментарий/решение(1)