Ильясов С.

Задача №1. Две пересекающиеся в точках

$X$ и

$Y$ окружности

$\omega_1$ и

$\omega_2$ находятся внутри окружности

$\Omega$ и касаются ее в точках

$A$ и

$B$ . Прямая

$AB$ повторно пересекает окружности

$\omega_1$ и

$\omega_2$ в точках

$A_1$ и

$B_1$ , соответственно. Вписанная в криволинейный треугольник

$A_1B_1X$ окружность касается стороны

$A_1B_1$ в точке

$Z$ . Докажите, что

$\angle AXZ=\angle BXZ$ .

( Ильясов С. )
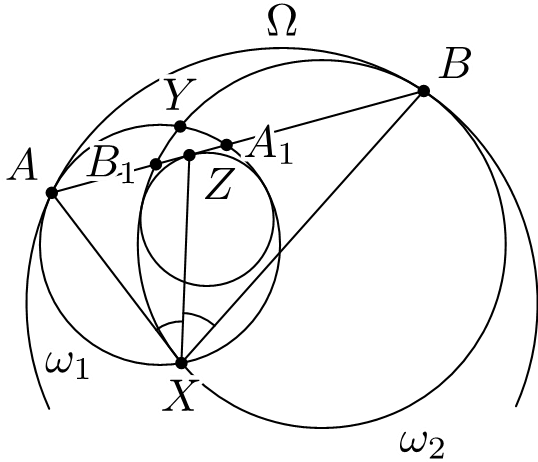
комментарий/решение(2) олимпиада

Задача №2. Клетчатую таблицу

$n \times n$ (где

$n \geq 2$ ) покрывают уголками, состоящими из трёх единичных клеток (уголок можно неоднократно поворачивать на

$90{}^\circ$ ) так, чтобы выполнялись следующие условия:
1) каждая клетка таблицы покрыта хотя бы одним из уголков;
2) две соседние по стороне клетки, покрытые одним уголком, не могут быть одновременно покрыты другим.
Каково наибольшее возможное число уголков в таком покрытии? ( Ильясов С. )
комментарий/решение(3) олимпиада

Задача №3. Найдите все такие пары натуральных чисел

$(n,k)$ , что число

$(n+1)(n+2) \dots (n+k)-k$ является полным квадратом. ( Ильясов С., Овчинников Д. )
комментарий/решение(4) олимпиада

Задача №4. На плоскости заданы 2015 точек, никакие три из которых не лежат на одной прямой и никакие четыре на одной окружности. Рассмотрим окружности, проходящие через три точки из данного множества и разбивающие остальные пополам, то есть 1006 лежит внутри окружности, а 1006 вне нее. Докажите, что найдутся хотя бы три окружности из рассмотренных, которые пересекающиеся по двум точкам из данного множества. ( Ильясов С. )
комментарий/решение олимпиада

Задача №5. На плоскости заданы 2015 точек, никакие три из которых не лежат на одной прямой и никакие четыре на одной окружности. Рассмотрим окружности, проходящие через три точки из данного множества и разбивающие остальные пополам, то есть 1006 лежит внутри окружности, а 1006 вне нее. Докажите, что найдутся хотя бы три окружности из рассмотренных, пересекающиеся по двум точкам из данного множества. ( Ильясов С. )
комментарий/решение(1) олимпиада

Задача №6. Найдите все такие пары натуральных чисел

$(n,k)$ , что число

$(n+1)(n+2) \dots (n+k)-k$ является полным квадратом. ( Ильясов С., Овчинников Д. )
комментарий/решение(6) олимпиада

Задача №7. Треугольник

$ABC$ вписан в окружность

$\Gamma$ . Вписанная в треугольник окружность касается стороны

$BC$ в точке

$N$ .

$\omega$ — окружность, вписанная в сегмент

$BAC$ окружности

$\Gamma$ , и проходящая через точку

$N$ . Пусть точки

$O$ и

$J$ — центры окружностей

$\omega$ и вневписанной окружности (касающейся стороны

$BC$ ), соответственно. Докажите, что прямые

$AO$ и

$JN$ параллельны. ( Ильясов С. )
комментарий/решение(4) олимпиада

Задача №8. Пусть

$O$ — центр окружности, описанной около остроугольного треугольника

$ABC$ . Рассмотрим две окружности

$\omega$ и

$\Omega$ , вписанные в угол

$BAC$ таким образом, что

$\omega$ касается внешним образом дуги

$BOC$ окружности, описанной около треугольника

$BOC$ ; а окружность

$\Omega$ касается внутренним образом окружности, описанной около треугольника

$ABC$ . Докажите, что радиус

$\Omega$ вдвое больше радиуса

$\omega$ . ( Ильясов С. )
комментарий/решение(1) олимпиада

Задача №9. Какое наибольшее число монет можно расставить в клетках таблицы

$n \times n$ (в каждой клетке таблицы может находиться не более одной монеты) так, чтобы любая монета не была одновременно ниже и правее чем любая другая? ( Ильясов С. )
комментарий/решение(1) олимпиада

Задача №10. Первый ученик расставил числа

$1$ ,

$2$ ,

$\ldots$ ,

$2015$ по кругу и выписал в тетрадь неотрицательные разности всех пар соседних чисел. Второй ученик должен выбрать из этих разностей наименьшую. Ему интересно, какое самое большое число он может получить? ( Ильясов С. )
комментарий/решение(1) олимпиада

Задача №11. Высоты

$AA_1$ и

$CC_1$ , остроугольного треугольника

$ABC$ пересекаются в точке

$H$ . На высоте

$AA_1$ отмечена точка

$P$ такая, что

$A_1P=AH$ , на высоте

$CC_1$ , отмечена точка

$Q$ такая, что

$C_1Q=CH$ . Докажите, что перпендикуляры к прямым

$AA_1$ и

$CC_1$ , проходящие через точки

$P$ и

$Q$ соответственно, пересекаются на описанной окружности треугольника

$ABC$ . ( Ильясов С. )
комментарий/решение(1) олимпиада

Задача №12. Рассмотрим всевозможные наборы натуральных чисел

$(x_1,x_2, \ldots,x_{100})$ такие, что

$1 \le x_i \le 2017$ для каждого

$i =1, 2, \ldots, 100$ . Будем говорить, что набор

$(y_1,y_2, \ldots,y_{100})$ больше набора

$(z_1,z_2, \ldots,z_{100})$ , если

$y_i > z_i$ для каждого

$i =1, 2, \ldots, 100$ . Какое наибольшее число наборов можно выписать на доску так, чтобы никакой набор не был больше никакого другого? ( Ильясов С., Аманкельды А. )
комментарий/решение(1) олимпиада

Задача №13. Дана функция

$f:\mathbb{Z}\to \mathbb{Z}$ такая, что для любых целых

$x$ и

$y$ выполнено

$f\left( x-f\left( y \right) \right)-f\left( 2x-f\left( y \right) \right)=f{{\left( x \right)}^{2}}.$ Докажите, что для всех целых

$x$ справедливо равенство

$f\left( f\left( x \right) \right)=0$ . Здесь

$\mathbb{Z}$ — множество целых чисел. ( Ильясов С. )
комментарий/решение(2) олимпиада

Задача №14. Дан выпуклый n-угольник

$M$ . Пусть

$k$ – наименьшее число точек, которое можно отметить внутри

$M$ так, чтобы внутри любого пятиугольника, вершины которого являются вершинами

$M$ , оказалось ровно 3 точки из отмеченных. Докажите, что

$k\ge n-2$ . («внутри» означает строго внутри, не на границе) ( Ильясов С. )
комментарий/решение(4) олимпиада

Задача №15. Найдите все функции

$f:\mathbb{N}\to \mathbb{N}$ , удовлетворяющие следующим условиям:
(a) существует бесконечно много попарно различных конечных множеств

$S$ таких, что для любого

$k\in S$ ,

$f\left( k \right)$ также

$\in S$ ;
(b) для любых различных

$m,n\in \mathbb{N}.$

$m-n | f\left( m \right)-f\left( n \right)$ . (Знак «|» означает делит; по другому, если

$a|b$ , то

$b$ делится на

$a$ .) ( Ильясов С. )
комментарий/решение(1) олимпиада

Задача №16. В правильном

$n$ -угольнике (

$n\ge4$ ) каждая диагональ красится в один из двух цветов. Затем в каждой паре одноцветных пересекающихся диагоналей удаляют одну из этих диагоналей. Какое наибольшее число диагоналей могло остаться при таких операциях? (Диагонали, выходящие из одной вершины, пересекающимися не считаются.) ( Ильясов С. )
комментарий/решение(5) олимпиада

Задача №17. Множество

$\Phi$ состоит из конечного числа точек на плоскости. Расстояние между любыми двумя точками из

$\Phi$ по крайней мере

$\sqrt{2}$ . Известно, что вырезанным из бумаги правильным треугольником со стороной

$3$ можно накрыть все точки множества

$\Phi$ . Из какого наибольшего количества точек может состоять

$\Phi$ ? ( Ильясов С. )
комментарий/решение(1) олимпиада

Задача №18. Пусть

$\mathbb{Q}$ — множество всех рациональных чисел. Найдите все функции

$f:\mathbb{Q}\rightarrow \mathbb{Q}$ такие, что для любых

$x, y\in\mathbb{Q}$ выполнено равенство

$f(x+y)-f(y)=f(f(x-y)+f(y)).$ ( Ильясов С. )
комментарий/решение(5) олимпиада

Задача №19. Множество

$\Phi$ состоит из конечного числа точек на плоскости. Расстояние между любыми двумя точками из

$\Phi$ по крайней мере

$\sqrt{2}$ . Известно, что вырезанным из бумаги правильным треугольником со стороной

$3$ можно накрыть все точки множества

$\Phi$ . Из какого наибольшего количества точек может состоять

$\Phi$ ? ( Ильясов С. )
комментарий/решение(9) олимпиада

Задача №20. Касательная прямая

$l$ к описанной окружности остроугольного треугольника

$ABC$ пересекает прямые

$AB$ ,

$BC$ и

$CA$ в точках

$C'$ ,

$A'$ и

$B'$ соответственно. Пусть

$H$ ---ортоцентр треугольника

$ABC$ . На прямых

$A'H$ ,

$B'H$ и

$C'H$ соответственно отмечены точки

$A_1$ ,

$B_1$ и

$C_1$ (отличные от

$H$ ) такие, что

$AH=AA_1$ ,

$BH=BB_1$ и

$CH=CC_1$ . Доказать, что окружности, описанные около треугольников

$ABC$ и

$A_1B_1C_1$ , касаются. ( Ильясов С. )
комментарий/решение(1) олимпиада

Задача №21. Вписанная окружность треугольника

$ABC$ касается сторон

$AB, BC, CA$ в точках

$C_0, A_0, B_0$ , соответственно. Пусть точка

$M$ — середина отрезка, соединяющего вершину

$C_0$ с точкой пересечения высот треугольника

$A_0B_0C_0$ , точка

$N$ — середина дуги

$ACB$ описанной окружности треугольника

$ABC$ . Докажите, что прямая

$MN$ проходит через центр вписанной окружности треугольника

$ABC$ . ( Ильясов С. )
комментарий/решение(7) олимпиада