К. Кохась
Задача №1. Докажите, что при $x$, $y$, $z > {3\over 2}$ выполнено неравенство ${x^{24}} + {\rm{ }}\sqrt[5]{{{y^{60}} + {z^{40}}}} \ge {\left( {{x^4}{y^3} + \frac{1}{3}{y^2}{z^2} + \frac{1}{9}{x^3}{z^3}} \right)^2}.$ ( К. Кохась )
комментарий/решение(1) олимпиада
Задача №2. Из натуральных чисел от 1 до 501 выбрано 250 чисел. Докажите, что для любого целого $t$ найдутся такие четыре выбранных числа $a_1$, $a_2$, $a_3$ и $a_4$, что $a_1 + a_2 + a_3 + a_4 -t $ делится на 23. ( К. Кохась )
комментарий/решение олимпиада
Задача №3. Во всех клетках таблицы $10\times 10$ записаны положительные числа. На некоторых 5 клетках сидят лягушки, заслоняя числа в этих клетках. Костя посчитал сумму всех видимых чисел и получил $10$. Потом каждая лягушка перепрыгнула в соседнюю по стороне клетку, и Костя насчитал сумму $10^{2}$. Потом лягушки снова прыгнули, и у Кости получилась сумма $10^{3}$, и т.д. — каждая новая сумма оказывалась в 10 раз больше предыдущей. Какую наибольшую сумму мог получить Костя? ( К. Кохась )
комментарий/решение олимпиада
Задача №4. В клетках таблицы $6\times 6$ стоят квадратные трехчлены с положительными старшими коэффициентами. Все их 108 коэффициентов — целые числа от $-60$ до $47$ (по одному разу). Докажите, что хотя бы в одном столбце сумма квадратных трехчленов имеет корень. ( К. Кохась, Ф. Петров )
комментарий/решение олимпиада
Задача №5. На столе лежит 100 куч камней. Два игрока делают ходы по очереди. За один ход разрешается взять со стола произвольное (ненулевое) количество камней из любого числа куч, не превосходящего 99. Проигрывает тот, кто не может сделать ход. Для любого начального положения укажите, кто выиграет при правильной игре — начинающий или его противник. ( К. Кохась )
комментарий/решение(1) олимпиада
Задача №6. Четыре мудреца стоят по кругу возле непрозрачного баобаба. На каждом из мудрецов красная, синяя или зеленая шляпа. Мудрец видит только двух соседних по кругу мудрецов. Мудрецы одновременно должны высказать предположение о цвете своей шляпы. Если хотя бы один из мудрецов угадал, они выиграли. Мудрецы имели возможность обсудить ситуацию до начала игры. Как им действовать, чтобы выиграть? ( К. Кохась )
комментарий/решение олимпиада
Задача №7. На столе лежит 100 куч камней. Два игрока делают ходы по очереди. За один ход разрешается взять со стола произвольное (ненулевое) количество камней из любого числа куч, не превосходящего 99. Проигрывает тот, кто не может сделать ход. Для любого начального положения укажите, кто выиграет при правильной игре — начинающий или его противник. ( К. Кохась )
комментарий/решение(1) олимпиада
Задача №8. Даны целые числа $0\leq b\leq c\leq d\leq a$, причем $a > 14$. Докажите, что не всякое натуральное число $n$ можно записать в виде $$ n=x(ax + b) + y(ay + c) + z(az + d), $$ где $x$, $y$, $z$ — некоторые целые числа. ( К. Кохась )
комментарий/решение(1) олимпиада
Задача №9. Внутри выпуклого четырехугольника с последовательными сторонами 3, 6, 5, 8 расположен круг. Докажите, что его радиус меньше 3. ( К. Кохась )
комментарий/решение(1) олимпиада
Задача №10. На левом берегу реки Лены стоят $m$ деревень, на правом — $n$ деревень, и ещё одна деревня стоит на острове. Известно, что $(m+1, n+1) > 1$. Между каждыми двумя деревнями, разделёнными водой, ходит паром с натуральным номером.
Жители каждой деревни утверждают, что все номера паромов, которые плавают в их деревню, различны, и эти номера составляют отрезок натурального ряда. Докажите, что хотя бы в одной деревне жители ошибаются. ( К. Кохась )
комментарий/решение олимпиада
Задача №11. Квадратный трехчлен $P(x)$, имеющий два вещественных корня, для всех $x$ удовлетворяет неравенству $P(x^3+x)\geq P(x^2+1)$. Найдите сумму корней трехчлена $P(x)$. ( А. Голованов, К. Кохась, М. Иванов )
комментарий/решение(2) олимпиада
Задача №12. Докажите, что при $x$, $y$, $z\geq 1$ выполнено неравенство $(x^3+2y^2+3z)(4y^3+5z^2+6x)(7z^3+8x^2+9y) \geq 720(xy+yz+xz).$ ( К. Кохась )
комментарий/решение(2) олимпиада
Задача №13. Докажите, что при $x$, $y$, $z\geq 1$ выполнено неравенство $(x^3+2y^2+3z)(4y^3+5z^2+6x)(7z^3+8x^2+9y) \geq 720(xy+yz+xz).$ ( К. Кохась )
комментарий/решение(2) олимпиада
Задача №14. Прямоугольник $1\times 5n$ клеток разбивают на плитки, каждая из которых — это либо отдельная клетка, либо «рваная доминошка», которая состоит из двух клеток, между которыми лежит четыре клетки (не принадлежащие этой доминошке). Докажите, что количество таких разбиений является точной пятой степенью. ( К. Кохась )
комментарий/решение олимпиада
Задача №15. В узлах клетчатой решетки по спирали расставляют числа $1,2,3 \ldots$ (см. рисунок). Потом в центре каждой клетки пишут сумму чисел в ее узлах. Докажите, что для любого натурального $n$ в центрах клеток бесконечно много раз встретятся числа, делящиеся на $n$.
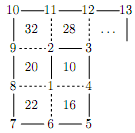
комментарий/решение олимпиада
Задача №16. По кругу стоит $3 n$ человек — это $n$ семей «мама-папа-ребенок». Любые два человека, стоящие рядом, могут поменяться местами, кроме случая, когда ребёнок меняется местом с одним из своих родителей (это не разрешено). При каких $n$ с помощью таких обменов людей можно расставить по кругу в любом порядке? (Перестановки, отличающиеся циклическим сдвигом, считаются различными.) ( К. Кохась )
комментарий/решение олимпиада