Д. Елиусизов
Задача №1. Для любого натурального числа докажите, что все его натуральные делители можно расставить по кругу так, чтобы из любых двух соседних чисел одно число делилось на другое. ( Д. Елиусизов )
комментарий/решение(1) олимпиада
Задача №2. Дано натуральное $N$. Докажите, что все натуральные делители числа $N$ можно выписать в последовательность $d_1$, $\ldots$, $d_k$ так, чтобы для каждого $1\le i < k$ одно из чисел $d_i/d_{i+1}$ и $d_{i+1}/d_i$ было простым. ( Д. Елиусизов )
комментарий/решение(1) олимпиада
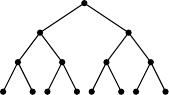
Задача №3. Дано дерево полного пирамидального вида, которое состоит из ${n+1}$ уровней, и из каждой вершины исходит два ребра вниз и входит одно ребро сверху (при этом в самую верхнюю вершину уровня 1 не входит ни одно ребро, а из вершин последнего $(n+1)$-го уровня не исходят рёбра). На рисунке ниже пример показан для $n = 3$. Сколько существует способов раскрасить ребра данного дерева в заданные $2^n$ цветов (каждое ребро покрашено в один цвет) так, чтобы для каждого цвета все рёбра, покрашенные в этот цвет, составляли путь из некоторой вершины в вершину последнего уровня? (Путь — это последовательность вершин, где каждая следующая вершина соединена ребром с предыдущей и находится уровнем ниже. )
комментарий/решение(3) олимпиада
Задача №4. Из доски $2^n \times 2^n$ ($n \geq 3$) вырезали одну клетку. Докажите, что оставшуюся часть доски можно покрыть без наложений уголками из 3-х клеток по крайней мере $3^{{4^{n-3}}}$ различными способами. ( Д. Елиусизов )
комментарий/решение олимпиада
Задача №5. Из доски $2^n \times 2^n$ ($n \geq 3$) вырезали одну клетку. Докажите, что оставшуюся часть доски можно покрыть без наложений уголками из 3-х клеток по крайней мере $4^{3 \cdot 4^{n-3}}$ различными способами. ( Д. Елиусизов )
комментарий/решение(1) олимпиада
Задача №6. Две черепахи одновременно выходят из точки с координатами $(0, 0)$ и на каждом шагу одновременно переходят на одну из целочисленных координат вверх или вправо (то есть из ${(x, y)}$ в ${(x+1,y)}$ или в ${(x,y+1)}$). Сколько существует способов им добраться до точки $(n, n)$, если последний раз они встречались только в точке $(0, 0)$? ( Д. Елиусизов )
комментарий/решение(1) олимпиада
Задача №7. Две черепахи одновременно выходят из точки с координатами $(0, 0)$ и на каждом шагу одновременно переходят на одну из целочисленных координат вверх или вправо (то есть из ${(x, y)}$ в ${(x+1,y)}$ или в ${(x,y+1)}$). Сколько существует способов им добраться до точки $(n, n)$, если последний раз они встречались только в точке $(0, 0)$? ( Д. Елиусизов )
комментарий/решение(3) олимпиада
Задача №8. Дано множество $A = \{1, 2, \ldots, n\}$ и натуральное число $m$. Сколько существует способов разделить $А$ на $m$ частей так, что если числа $a < b$ лежат в одной части, а $c < d$ в другой, то $(a-d)(b-c) > 0$? Например, если $n = 4$, $m = 2$, то существует 5 способов разделения: $$ \{1, 2\} \{3, 4\}; \quad \{1, 2, 3\} \{4\}; \quad \{1, 2, 4\} \{3\}; \quad \{1, 3, 4\} \{2\}; \quad \{2, 3, 4\} \{1\}. $$ ( Д. Елиусизов )
комментарий/решение(3) олимпиада
Задача №9. Назовем квадратную таблицу бинарной, если в каждой ее клетке записано одно число $0$ или $1$. Бинарная таблица называется регулярной, если в каждой ее строке и в каждом столбце ровно по 2 единицы. Определите количество регулярных таблиц размером $n\times n$ ($n > 1$ — данное фиксированное натуральное число). (Можно считать, что строки и столбцы таблиц пронумерованы: случаи совпадения при повороте, отражения и т.п. считать различными). ( Д. Елиусизов )
комментарий/решение(1) олимпиада
Задача №10. Даны нечетные натуральные числа $m > 1$, $k$ и простое число $p$ такое, что $p > mk+1$. Докажите, что сумма $$ (C_k^k)^m+(C_{k+1}^k)^m+ \ldots +(C_{p-1}^k)^m \quad \text{делится на} \quad p^2. $$ Здесь $C_n^k=\frac{n!}{k!(n-k)!}$ — биномиальный коэффициент. ( Д. Елиусизов )
комментарий/решение(1) олимпиада
Задача №11. Докажите, что для любых действительных чисел $a_1$, $a_2$, $\dots$, $a_n$, $b_1$, $b_2$, $\dots$, $b_n$ выполнено неравенство $$ \left (a_1^{2010}+a_2^{2010} +\ldots+a_n^{2010}\right) \left (b_1^{2010}+b_2^{2010} + \ldots +b_n^{2010}\right) \geq \left (a_1b_1^{2009}+a_2b_2^{2009}+ \ldots+a_nb_n^{2009}\right) \left (a_1^{2009}b_1+a_2^{2009}b_2 +\ldots+a_n^{2009}b_n\right). $$ ( Д. Елиусизов )
комментарий/решение(1) олимпиада
Задача №12. Последовательность $\{a_n\}_{n\geq1}$ определена следующим образом: $a_1 =\alpha $ и $a_{n+1} = 2a_n^2-1$ для $n\geq 1$. Сколько различных значений может принимать действительное число $\alpha$, если $a_{2010} = 0$? ( Д. Елиусизов )
комментарий/решение(1) олимпиада
Задача №13. Дан треугольник $ABC$. Рассмотрим эллипс $\Omega_1$, проходящий через точку $C$, у которого фокусы расположены в точках $A$ и $B$. Аналогичным образом определим эллипсы $\Omega_2,\Omega_3$ (с фокусами $B,C$ и $C,A$ соответственно). Докажите, что если все три эллипса проходят через одну общую точку $D$, то точки $A,B,C,D$ лежат на одной окружности (эллипсом называется геометрическое место точек, суммарное расстояние от которых до 2-х фиксированных точек, называемых фокусами, есть постоянная величина). ( Д. Елиусизов )
комментарий/решение(1) олимпиада
Задача №14. Докажите, что для чисел $ 0 < a_{1}\leq a_{2}\leq \dots \leq a_{n} $ ($ n\geq 3$) выполнено неравенство $$ \frac{a_{1}^{2}}{a_{2}}+\frac{a_{2}^{3}}{a_{3}^{2}}+\ldots+\frac{a_{n}^{n+1}}{a_{1}^{n}}\geq a_{1}+a_{2}+ \ldots +a_{n}. $$ ( Д. Елиусизов )
комментарий/решение(2) олимпиада
Задача №15. Для натурального числа $k$ обозначим через $F_k$ — множество всех связанных плоских фигур, состоящих ровно из $k$ единичных клеток. Для произвольной плоской фигуры $f$ через $S(f)$ обозначим наименьшую возможную площадь прямоугольника, содержащего внутри себя $f$. Для заданного $n$ натурального определите $\mathop {\max }\limits_{f \in F_n } S\left( f \right)$. ( Д. Елиусизов )
комментарий/решение олимпиада
Задача №16. Функция $f:\mathbb{R} \to \mathbb{R}$, где $\mathbb{R}$ — поле вещественных чисел, удовлетворяет тождеству $f(f(x)+x+y)=2x+f(y)$ для любых $x,y\in \mathbb{R}$. ( Д. Елиусизов, Е. Байсалов )
комментарий/решение(3) олимпиада
Задача №17. Докажите неравенство $ab + bc + ac \geq 2(a + b + c)$ для положительных действительных чисел $a$, $b$, $c$ если известно, что $a + b + c + 2 = abc$. ( Д. Елиусизов )
комментарий/решение(1) олимпиада
Задача №18. Найдите все функции $f:\mathbb{R}\to \mathbb{R}$, где $\mathbb{R}$ — поле вещественных чисел, удовлетворяющие тождеству $f(xy+f(x))=xf(y)+f(x)$ для любых $x,y\in \mathbb{R}$. ( Д. Елиусизов )
комментарий/решение(2) олимпиада
Задача №19. Докажите неравенство $ab + bc + ac \geq 2(a + b + c)$ для положительных действительных чисел $a$, $b$, $c$ если известно, что $a + b + c + 2 = abc$. ( Д. Елиусизов )
комментарий/решение(1) олимпиада
Задача №20. Пусть $P(n)$ это количество способов разбить натуральное число $n$ на сумму степеней двойки, при этом порядок не имеет значение. Например $P(5) = 4$, так как $5=4+1=2+2+1=2+1+1+1=1+1+1+1+1$. Докажите, что для любого натурального $n$ верно тождество $$P(n) + (-1)^{a_1} P(n-1) + (-1)^{a_2} P(n-2) + \ldots + (-1)^{a_{n-1}} P(1) + (-1)^{a_n} = 0,$$ где $a_k$ — количество единиц в двоичной записи числа $k$. ( Д. Елиусизов )
комментарий/решение(2) олимпиада
Задача №21. В каждую клетку таблицы $4 \times4$, в которой строки помечены числами $1,2,3,4$, а столбцы — буквами $a,b,c,d$, записано одно число: $0$ или $1$. Такая таблица называется допустимой, если в каждой ее строке и в каждом столбце стоят ровно по две единицы. Определите количество допустимых таблиц. ( Д. Елиусизов )
комментарий/решение(2) олимпиада
Задача №22. Докажите, что для положительных действительных чисел $a, b$ и $c$, для которых $abc \le 1$, выполнено неравенство $$\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c} \ge 1 + \dfrac{6}{a+b+c}.$$ ( Д. Елиусизов )
комментарий/решение(13) олимпиада
Задача №23. Определите все многочлены $P(x)$ с действительными коэффициентами такие, что для любого рационального $r$ уравнение $P(x) = r$ имеет рациональное решение. ( Д. Елиусизов )
комментарий/решение(1) олимпиада
Задача №24. Дан (неориентированный) граф (без петель) с $2n$ вершинами и с $2n(n-1)$ ребрами, $n > 1$. Докажите, что некоторые вершины и ребра этого графа можно покрасить в красный цвет так, чтобы каждое красное ребро соединяло красные вершины и из каждой красной вершины исходило ровно $n$ красных ребер. ( Д. Елиусизов )
комментарий/решение(1) олимпиада
Задача №25. В треугольнике $ABC$ точки $A_0, B_0$ и $C_0$ — середины сторон $BC, CA$ и $AB$ соответственно, а точки $A_1, B_1$ и $C_1$ — середины (по длине) ломаных $BAC, CBA$ и $BCA$ соответственно. Докажите, что прямые $A_0A_1, B_0B_1$ и $C_0C_1$ пересекаются в одной точке. ( Д. Елиусизов )
комментарий/решение(1) олимпиада
Задача №26. Найдите максимальное значение вещественного числа $M$, при котором для любых положительных вещественных чисел $a,b,c$ выполняется неравенство $$a^3 + b^3 + c^3 - 3abc \ge M (|a-b|^3 + |b - c|^3 + |c - a|^3)$$ ( Д. Елиусизов )
комментарий/решение(1) олимпиада
Задача №27. Пусть вписанная окружность $\omega$ треугольника $ABC$ касается стороны $BC$ в точке $K$. Проведем окружность, проходящую через точки $B$ и $C$, и касающуюся $\omega$ в точке $S$. Докажите, что прямая $SK$ проходит через центр вневписанной окружности треугольника $ABC$, касающейся стороны $BC$. ( Д. Елиусизов )
комментарий/решение олимпиада
Задача №28. Пусть $a_1, a_2, \dots, a_n$ — арифметическая прогрессия целых чисел такая, что $a_i$ делится на $i$ для всех $i=1, 2, \dots , n-1$ и $a_n$ не делится на $n$. Докажите, что $n$ — степень простого числа. ( Д. Елиусизов )
комментарий/решение(1) олимпиада
Задача №29. Для действительных чисел $x, y, z \in (0;1)$ известно, что $8xyz = (1 - x)(1 - y)(1 - z)$. Докажите, что $x+y+z \geq 1$. ( Д. Елиусизов )
комментарий/решение(1) олимпиада
Задача №30. Кузнечик стоит на координатной оси в точке с координатой 0. На каждом шагу ему разрешается прыгнуть из точки с координатой $x$ в точку с координатой $x + 1$, либо в точку с координатой $2x$. Весом координаты назовем минимальное количество прыжков, требуемое кузнечику для ее достижения. Определите координату $x < 2010$ с наибольшим весом. ( Д. Елиусизов )
комментарий/решение олимпиада
Задача №31. Пусть $N={{10}^{10}}-1$. Докажите, что существует перестановка $({{a}_{1}},{{a}_{2}},\ldots ,{{a}_{N}})$ чисел $(1,2,\ldots ,N)$ такая, что $$\{|{{a}_{1}}-{{a}_{2}}|, |{{a}_{2}}-{{a}_{3}}|, |{{a}_{3}}-{{a}_{4}}|,\dots, |{{a}_{N-1}}-{{a}_{N}}|\}=\{1,10,{{10}^{2}}, {{10}^{3}},\dots, {{10}^{9}}\}.$$ (Какие-то из разностей $\left| {{a}_{i}}-{{a}_{i+1}} \right|$ могут принимать одинаковые значения, но при этом все значения множества $\{1,10, {{10}^{2}}, {{10}^{3}},\dots, {{10}^{9}}\}$ должны встречаться среди этих разностей). ( Д. Елиусизов )
комментарий/решение олимпиада
Задача №32. Обозначим через $A_n$ множество разбиений последовательности $1, 2, \dots, n$ на несколько подпоследовательностей, в каждой из которых любые два соседних члена имеют разную чётность, а через $B_n$ — множество разбиений последовательности $1, 2, \dots, n$ на несколько подпоследовательностей, в каждой из которых все члены имеют одинаковую чётность (например, разбиение $\{(1, 4, 5, 8), (2, 3), (6, 9), (7)\}$ является элементом $A_9$, а разбиение $\{(1, 3, 5), (2, 4), (6)\}$ является элементом $B_6$). Докажите, что при каждом натуральном $n$ множества $A_n$ и $B_{n+1}$ содержат одинаковое количество элементов. ( Д. Елиусизов )
комментарий/решение(1) олимпиада
Задача №33. Дано натуральное число $n$. Докажите неравенство $\displaylines{\sum_{i=1}^{n}\frac{1}{i(i+1)(i+2)(i+3)(i+4)} < \frac{1}{96}.}$ ( Д. Елиусизов )
комментарий/решение(2) олимпиада
Задача №34. Назовем натуральное число абсолютно простым, если произвольно переставляя его цифры, мы будем всегда получать простое число. Например, число 113 абсолютно простое (113, 131, 311 - все простые). Докажите, что не существует абсолютно простого числа, десятичная запись которого содержит все цифры 1, 3, 7, 9. ( Д. Елиусизов )
комментарий/решение(1) олимпиада
Задача №35. Определите все пары натуральных чисел $m, n,$ удовлетворяющих равенству $(2^m + 1, 2^n + 1) = 2^{(m, n)} + 1. $ Здесь $(a, b)$ — это наибольший общий делитель чисел $a, b$. ( Д. Елиусизов )
комментарий/решение(1) олимпиада
Задача №36. Определите все пары положительных действительных чисел $(\alpha, \beta)$ для которых существует функция $f:\mathbb{R}^+\rightarrow \mathbb{R} ^+$ удовлетворяющая для всех положительных действительных чисел $x$ уравнению $f(f(x))=\alpha f(x)-\beta x.$ ( Д. Елиусизов )
комментарий/решение(1) олимпиада
Задача №37. Докажите, что для любого простого числа $p$ существуют бесконечно много четверок $(x, y, z, t)$ попарно различных натуральных чисел таких, что число $(x^2+p t^2)(y^2+p t^2)(z^2+p t^2)$ является полным квадратом. ( Д. Елиусизов, Е. Байсалов )
комментарий/решение(1) олимпиада
Задача №38. Дано натуральное число $m\geq2.$ Последовательность натуральных чисел $(b_0,b_1,\ldots,b_m)$ назовем вогнутой, если $b_k+b_{k-2}\le2b_{k-1}$ для всех $2\le k\le m.$ Докажите, что существует не более $2^m$ вогнутых последовательностей, начинающихся с $b_0=1$ и $b_1=2.$ ( Д. Елиусизов )
комментарий/решение(1) олимпиада
Задача №39. Докажите, что существует по крайней мере $100!$ способов разбить число $100!$ на сумму слагаемых из множества $\{1!, 2!, 3!, \ldots, 99! \}$. (Разбиения, отличающиеся порядком слагаемых, считаются одинаковыми; любое слагаемое можно использовать несколько раз. Напомним, что $n!=1 \cdot 2 \cdot \ldots \cdot n.$) ( Д. Елиусизов )
комментарий/решение(2) олимпиада
Задача №40. Последовательность $\{a_n\}$ определена следующим образом: $a_0=1$ и ${a_n} = \sum\limits_{k = 1}^{[\sqrt n ]} {{a_{n - {k^2}}}}$ для $n \ge 1.$ Докажите, что среди $a_1,a_2,\ldots,a_{10^6}$ есть хотя бы 500 четных чисел. (Здесь $[x]$ обозначает наибольшее целое, не превосходящее $x$.) ( Д. Елиусизов )
комментарий/решение(2) олимпиада