Ф. Бахарев

Задача №1. В окружность с центром

$O$ и радиусом 1 вписан остроугольный треугольник

$ABC$ , все углы которого больше

$45^\circ$ . Из точки

$B$ опущен перпендикуляр

$BB_1$ на прямую

$CO$ , а из точки

$B_1$ опущен перпендикуляр

$B_1B_2$ на прямую

$AC$ . Точно так же из точки

$C$ опущен перпендикуляр

$CC_1$ на прямую

$BO$ , а из точки

$C_1$ опущен перпендикуляр

$C_1C_2$ на прямую

$AB$ . Прямые

$B_1B_2$ и

$C_1C_2$ пересекаются в точке

$A_3$ . Аналогично определяются точки

$B_3$ и

$C_3$ . Найдите радиус описанной окружности треугольника

$A_3B_3C_3$ . ( Ф. Петров, Ф. Бахарев )
комментарий/решение олимпиада

Задача №2. Квадрат

$600\times 600$ разбит на фигурки из 4 клеток вида

В фигурках первых двух типов в закрашенных клетках записано число

$2^k$ , где

$k$ — номер столбца, в котором находится эта клетка. Докажите, что сумма всех записанных чисел делится на 9. ( Ф. Бахарев )
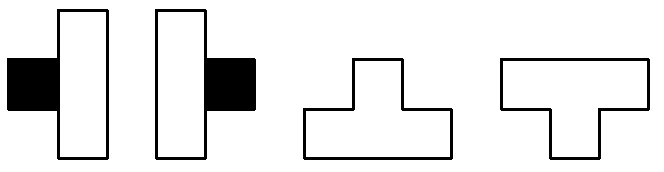
комментарий/решение(1) олимпиада

Задача №3. Точка

$O$ — центр описанной окружности остроугольного треугольника

$ABC$ . Некоторая окружность проходит через точки

$B$ и

$C$ и пересекает стороны

$AB$ и

$AC$ треугольника. На ее дуге, лежащей внутри треугольника, выбраны точки

$D$ и

$E$ так, что отрезки

$BD$ и

$CE$ проходят через точку

$O$ . Перпендикуляр

$DD_1$ к стороне

$AB$ и перпендикуляр

$EE_1$ к стороне

$AC$ пересекаются в точке

$M$ . Докажите, что точки

$A$ ,

$M$ и

$O$ лежат на одной прямой. ( Ф. Бахарев )
комментарий/решение(1) олимпиада

Задача №4. Точки

$H$ и

$M$ — ортоцентр и точка пересечения медиан остроугольного треугольника

$ABC$ . Точка

$B_1$ — середина дуги

$AC$ описанной окружности этого треугольника. Известно, что длина отрезка

$B_1M$ равна радиусу описанной окружности. Докажите, что

$BM\geq BH$ . ( Ф. Бахарев )
комментарий/решение олимпиада

Задача №5. На плоскости даны точки

$A$ и

$B$ , а также прямая

$\ell$ , проходящая через точку

$B$ . Рассмотрим произвольную окружность

$\omega$ , касающуюся прямой

$\ell$ в точке

$B$ и не содержащую внутри себя точку

$A$ . Касательные к

$\omega$ , проведенные из точки

$A$ , касаются

$\omega$ в точках

$X$ и

$Y$ . Докажите, что прямая

$XY$ проходит через фиксированную точку, не зависящую от выбора окружности

$\omega$ . ( Ф. Бахарев )
комментарий/решение(1) олимпиада

Задача №6. Точка

$I$ — центр вписанной окружности треугольника

$ABC$ . Точки

$B_1$ и

$C_1$ — середины сторон

$AC$ и

$AB$ соответственно. Известно, что

$\angle BIC_1 + \angle CIB_1 = 180^\circ$ . Докажите равенство

$AB+AC=3BC$ . ( Д. Ростовский, Ф. Бахарев )
комментарий/решение олимпиада

Задача №7. Внутри трапеции

$ABCD$

$(BC \parallel AD),$ где

$AD = 2BC,$ взята точка

$F,$ для которой

$AB = FB.$ Точка

$M$ — середина отрезка

$FD.$ Докажите, что

$CM \perp FA.$ ( Ф. Бахарев )
комментарий/решение(2) олимпиада