Олимпиада Туймаада по математике. Младшая лига. 2007 год

Квадрат $600\times 600$ разбит на фигурки из 4 клеток вида

В фигурках первых двух типов в закрашенных клетках записано число $2^k$, где $k$ — номер столбца, в котором находится эта клетка. Докажите, что сумма всех записанных чисел делится на 9. ( Ф. Бахарев )

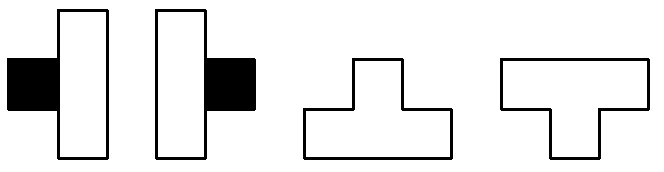
Комментарий/решение

Раскраска: Запишем в каждую клетку доски число $2^{n+2}$, где $n$ $-$ номер столбца, в котором находится эта клетка.

Тогда можно заметить что если $T$ сумма изначальных чисел в нашей доске, то mod 9 оно не изменилось. Отсюда следует, что

$$T \equiv 600(2^3+2^4+\dots+2^{602}) \equiv 0 \pmod{9}$$

ч.т.д.