Олимпиада Туймаада по математике. Старшая лига. 2004 год
Задача №1. Существуют ли такая последовательность действительных чисел
$a_1$, $a_2$, $a_3$, $\dots$ и такой непостоянный многочлен $P(x)$,
что $a_m+a_n=P(mn)$ для любых натуральных $m$ и $n$?
(
А. Голованов
)
комментарий/решение
комментарий/решение
Задача №2. На плоскости провели 100 прямых, никакие две из которых не
параллельны и никакие три не пересекаются в одной точке, и отметили
все точки их пересечения. После этого все прямые и $k$ отмеченных точек
стерли. При каком наибольшем $k$ по оставшимся точкам пересечения
заведомо можно восстановить исходные прямые?
(
А. Голованов
)
комментарий/решение
комментарий/решение
Задача №3. В окружность с центром $O$ и радиусом 1 вписан остроугольный
треугольник $ABC$, все углы которого больше $45^\circ$. Из точки $B$
опущен перпендикуляр $BB_1$ на прямую $CO$, а из точки $B_1$ опущен
перпендикуляр $B_1B_2$ на прямую $AC$. Точно так же из точки $C$ опущен
перпендикуляр $CC_1$ на прямую $BO$, а из точки $C_1$ опущен перпендикуляр
$C_1C_2$ на прямую $AB$. Прямые $B_1B_2$ и $C_1C_2$ пересекаются в точке
$A_3$. Аналогично определяются точки $B_3$ и $C_3$. Найдите радиус описанной
окружности треугольника $A_3B_3C_3$.
(
Ф. Петров,
Ф. Бахарев
)
комментарий/решение(1)
комментарий/решение(1)
Задача №4. В городе N. существует множество оппозиционных обществ, каждое из которых
состоит из 10 членов. Известно, что для любых 2004 обществ найдется человек,
состоящий хотя бы в 11 из них. Докажите, что правительство может
арестовать 2003 человека так, чтобы в каждом обществе хотя бы
один член был арестован.
(
Д. Карпов,
В. Дольников
)
комментарий/решение
комментарий/решение
Задача №5. 50 рыцарей короля Артура сидели за круглым столом. Перед каждым из
них стоял бокал красного или белого вина. Известно, что на столе
стоял хотя бы один бокал красного вина и хотя бы один бокал белого вина.
Король два раза хлопнул в ладоши. После первого хлопка каждый рыцарь, перед
которым стоял бокал красного вина, взял у своего левого соседа его бокал,
а после второго хлопка каждый рыцарь, перед которым стоял бокал
белого вина (и, возможно, что-нибудь еще), передал этот бокал
левому соседу своего левого соседа.
Докажите, что кто-то из рыцарей остался без вина.
(
А. Храбров
)
комментарий/решение
комментарий/решение
Задача №6. Вписанная окружность треугольника $ABC$ касается сторон $AB$ и $BC$ в
точках $P$ и $Q$. Прямая $PQ$ пересекает описанную окружность треугольника
$ABC$ в точках $X$ и $Y$. Найдите $\angle XBY$, если $\angle ABC = 90^\circ$.
(
А. Смирнов
)
комментарий/решение(2)
комментарий/решение(2)
Задача №7. В клетках доски $n \times n$ расставлены нули и единицы.
Во всех клетках левого столбца стоят единицы, и в каждой фигурке вида
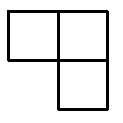 (состоящей из клетки и ее соседей слева и снизу) сумма чисел четна.
Докажите, что в таблице нет двух одинаковых строк.
(
О. Ванюшина
)
(состоящей из клетки и ее соседей слева и снизу) сумма чисел четна.
Докажите, что в таблице нет двух одинаковых строк.
(
О. Ванюшина
)
комментарий/решение
комментарий/решение
Задача №8. О натуральных числах $m$ и $n$ известно, что $m > n^{n-1}$ и все числа
$m+1$, $m+2$, $\dots$, $m+n$ — составные. Докажите, что существуют такие
различные простые числа $p_1$, $p_2$, $\dots$, $p_n$, что $m+k$ делится на
$p_k$ при $k = 1$, 2, $\dots$, $n$.
(
C.A.Grimm
)
комментарий/решение(1)
комментарий/решение(1)