Ф. Бахарев

Есеп №1. Центрі

$O$ нүктесі және радиусы 1 болатын шеңберге, барлық бұрыштары

$45{}^\circ$ -градустан үлкен сүйірбұрышты үшбұрыш іштей сызылды.

$B$ нүктесінен

$CO$ түзуіне

$B{{B}_{1}}$ перпендикуляры, ал

${{B}_{1}}$ нүктесінен

$AC$ түзуіне

${{B}_{1}}{{B}_{2}}$ перпендикуляры жүргізілді. Дәл осылай,

$C$ нүктесінен

$BO$ түзуіне

$C{{C}_{1}}$ перпендикуляры, ал

${{C}_{1}}$ нүктесінен

$AB$ түзуіне

${{C}_{1}}{{C}_{2}}$ перпендикуляры жүргізілді.

${{B}_{1}}{{B}_{2}}$ және

${{C}_{1}}{{C}_{2}}$ түзулері

${{A}_{3}}$ нүктесінде қиылысады. Дәл осылай

${{B}_{3}}$ және

${{C}_{3}}$ нүктелері анықталады.

${{A}_{3}}{{B}_{3}}{{C}_{3}}$ үшбұрышына сырттай сызылған шеңбердің радиусын табыңыз. ( Ф. Петров, Ф. Бахарев )
комментарий/решение олимпиада

Есеп №2.

$600\times 600$ шаршысы, 4 тордан тұратын (сурет)

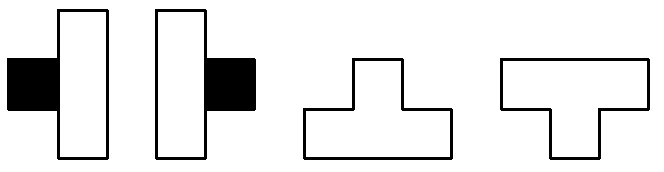түріндегі фигураларға бөлінген. Алғашқы екі фигура түріндегі фигураларда,

$k$ осы тор орналасқан баған нөмірі болатындай,

${{2}^{k}}$ саны жазылған. Барлық жазылған сандардың қосындысы 9-ға бөлінетінін дәлелдеңіз. ( Ф. Бахарев )
комментарий/решение(1) олимпиада

Есеп №3.

$O$ нүктесі,

$ABC$ үшбұрышына сырттай сызылған үшбұрыштың центрі. Бір шеңбер

$B$ және

$C$ нүктелері арқылы өтіп

$AB$ және

$AC$ қабырғаларын қияды. Осы шеңбердің, үшбұрыш ішінде орналасқан доғасының бойынан,

$BD$ және

$CE$ кесінділері

$O$ нүктесі арқылы өтетіндей,

$D$ және

$E$ нүктелері алынған.

$AB$ қабырғасына жүргізілген перпендикуляр

$D{{D}_{1}}$ және

$AC$ қабырғасына жүргізілген перпендикуляр

$E{{E}_{1}}$ ,

$M$ нүктесінде қиылысады.

$A$ ,

$M$ және

$O$ нүктелері бір түзудің бойында жататынын дәлелдеңіз. ( Ф. Бахарев )
комментарий/решение(1) олимпиада

Есеп №4.

$H$ және

$M$ нүктелері,

$ABC$ сүйірбұрышты үшбұрышының ортоцентрі және медианалардың қиылысу нүктесі.

${{B}_{1}}$ нүктесі, осы үшбұрышқа сырттай сызылған шеңбердің

$AC$ доғасының ортасы.

${{B}_{1}}M$ кесіндісінің ұзындығы сырттай сызылған шеңбердің радиусына тең екені белгілі.

$BM\ge BH$ екенін дәлелдеңіз. ( Ф. Бахарев )
комментарий/решение олимпиада

Есеп №5. Жазықтықта

$A$ және

$B$ нүктелері, және де

$B$ нүктесі арқылы өтетін

$l$ түзуі берілсін.

$l$ түзуімен

$B$ нүктесінде жанасатын және

$A$ нүктесін қамтымайтын кез-келген

$\omega$ шеңбері берілісін.

$\omega$ шеңберіне

$A$ нүктесі арқылы жүргізілген жанамалар осы шеңбермен

$X$ және

$Y$ нүктелерінде жанасады.

$XY$ түзуі,

$\omega$ шеңберінің таңдалымына тәуелсіз, бекітілген нүкте арқылы өтетінін дәлелдеңіз. ( Ф. Бахарев )
комментарий/решение(1) олимпиада

Есеп №6.

$I$ нүктесі

$ABC$ үшбұрышына іштей сызылған шеңбер центрі болсын.

$AC$ және

$AB$ қабырғаларының орталары сәйкес түрде

${{B}_{1}}$ және

${{C}_{1}}$ нүктелері болсын.

$\angle BI{{C}_{1}}+\angle CI{{B}_{1}}=180{}^\circ$ болатыны белгілі.

$AB+AC=3BC$ теңдігін дәлелде. ( Д. Ростовский, Ф. Бахарев )
комментарий/решение олимпиада

Есеп №7.

$ABCD$ трапециясында

$BC \parallel AD$ және

$AD = 2BC.$ Трапеция ішінде

$AB = FB$ болатындай

$F$ нүктесі белгіленген.

$M$ нүктесі —

$FD$ кесіндісінің ортасы.

$CM \perp FA$ екенін дәлелдеңіз. ( Ф. Бахарев )
комментарий/решение(2) олимпиада