18-я Международная Жаутыковская олимпиада по математике, 2022 год
Полные решения этих задач опубликованы в книге, доступный для заказа по ссылке
Задача №1. Ненулевые многочлены $P(x)$, $Q(x)$ и $R(x)$ с вещественными коэффициентами удовлетворяют тождествам $ P(x)+Q(x)+R(x)=P(Q(x))+Q(R(x))+R(P(x))=0. $ Докажите, что степени всех трёх многочленов чётны.
(
И. Богданов
)
комментарий/решение(2)
комментарий/решение(2)
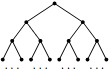
Задача №2. На плоскости нарисовано 10-этажное 2-дерево: отмечена вершина $A_1$, она соединена отрезками с двумя вершинами $B_1$ и $B_2$, каждая из которых соединена отрезками с двумя из четырех вершин $C_1, C_2, C_3, C_4$ (каждая из вершин $C_i$ соединена ровно с одной вершиной $B_j$); и так далее вплоть до 512 вершин $J_1,\dots,J_{512}$. Каждая вершина $J_1,\dots,J_{512}$ покрашена в один из двух цветов: голубой или золотой. Рассматриваются всевозможные перестановки $f$ множества вершин нарисованного дерева, такие что (i) если вершины $X$ и $Y$ были соединены отрезком, то вершины $f(X)$ и $f(Y)$ также соединены отрезком, и (ii) если вершина $X$ была покрашена в какой-то цвет, то вершина $f(X)$ покрашена в тот же цвет. Для какого максимального $M$ заведомо найдутся хотя бы $M$ различных рассматриваемых перестановок?
комментарий/решение(1)
комментарий/решение(1)
Задача №3. В параллелограмме $ABCD$ с острым углом $A$ на отрезке $AD$ отмечена точка $N$, а на отрезке $CN$ — точка $M$ так, что $AB=BM=CM$. Точка $K$ симметрична точке $N$ относительно прямой $MD$. Прямая $MK$ пересекает отрезок $AD$ в точке $L$. Пусть $P$ — общая точка описанных окружностей треугольников $AMD$ и $CNK$, причем точки $A$ и $P$ лежат по одну сторону от прямой $MK$. Докажите, что $\angle CPM=\angle DPL$.
(
М. Кунгожин
)
комментарий/решение(2)
комментарий/решение(2)
Задача №4. В треугольнике $ABC$ точка $M$ — середина стороны $AB$, а $I$ — центр вписанной окружности. Точка $A_1$ симметрична точке $A$ относительно прямой $BI$, а точка $B_1$ симметрична точке $B$ относительно прямой $AI$. Пусть $N$ — середина отрезка $A_1B_1$. Докажите, что $IN > IM$.
(
М. Кунгожин
)
комментарий/решение(1)
комментарий/решение(1)
Задача №5. Дан многочлен $f(x)$ с вещественными коэффициентами степени выше 1. Докажите, что существует бесконечно много натуральных чисел, не представимых в виде $f(n+1)+\dots+f(n+k)$ с натуральными $n$ и $k$.
(
А. Голованов
)
комментарий/решение(1)
комментарий/решение(1)
Задача №6. Существуют ли две ограниченные последовательности $a_1, a_2, \ldots$ и $b_1, b_2, \ldots$ такие, что для любых натуральных $m>n$ выполнено хотя бы одно из двух условий $|a_m-a_n|>{1\over\sqrt{n}}$ или$|b_m-b_n|>{1\over\sqrt{n}}?$
(
Шынтас Н.
)
комментарий/решение(1)
комментарий/решение(1)