18-я Международная Жаутыковская олимпиада по математике, 2022 год

На плоскости нарисовано 10-этажное 2-дерево: отмечена вершина $A_1$, она соединена отрезками с двумя вершинами $B_1$ и $B_2$, каждая из которых соединена отрезками с двумя из четырех вершин $C_1, C_2, C_3, C_4$ (каждая из вершин $C_i$ соединена ровно с одной вершиной $B_j$); и так далее вплоть до 512 вершин $J_1,\dots,J_{512}$. Каждая вершина $J_1,\dots,J_{512}$ покрашена в один из двух цветов: голубой или золотой. Рассматриваются всевозможные перестановки $f$ множества вершин нарисованного дерева, такие что (i) если вершины $X$ и $Y$ были соединены отрезком, то вершины $f(X)$ и $f(Y)$ также соединены отрезком, и (ii) если вершина $X$ была покрашена в какой-то цвет, то вершина $f(X)$ покрашена в тот же цвет. Для какого максимального $M$ заведомо найдутся хотя бы $M$ различных рассматриваемых перестановок?

( Г. Челноков )

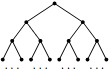
Комментарий/решение

Ответ: $2^{128}$

Задача состоит из двух частей. Сначала показать, что $M \geq 2^{128}$ для любой раскраски, а потом привести пример когда $M = 2^{128}$.

Сначала докажем оценку. Рассмотрим $4$ вершины $10$го этажа, которые имеют общею вершину на $8$ом этаже. Покажем, что при любой раскраске этих $4$ вершин существует хотя бы две перестановки. Пусть это не так. Значит есть ровно одна перестановка - тождественная. В этом случае в паре вершин которые имеют общею вершину на $9$ом этаже покрашены в разные цвета. Тогда мы можем переставить эти две пары вершин. Значит в каждой четверке вершин не менее двух перестановок. Так как у нашего графа $128$ таких четверок вершин которые никак не связаны между собой, то всего перестановок не менее $M \geq 2^{128}$.

Приведем пример для которого существует ровно $2^{128}$ перестановок. Для этого обозначим вершины золотого цвета как З, голубого как Г. Раз у нас ровно $2^{128}$ перестановок, то все перестановки должны быть внутри четверок вершин с общей вершиной на $8$ом этаже. Четверки вершин у которых ровно две перестановки это ЗГЗГ, ЗГЗЗ, ЗГГГ. Заметим, что никакие из этих двух раскрасок нельзя поменять местами, в виду различия количества вершин покрашенных в золотой цвет. Тогда создадим из них восьмерки вершин, просто комбинирую по парам эти раскраски. Мы получим три типа раскраски восьмерки вершин. которые нельзя поменять друг с другом местами. Аналогично мы получаем и $16$-верки вершин, и $32$-верки вершин и .... и $256$-верки вершин которые нельзя поменять местами между собой. Беря две $256$-верки вершин, мы получаем требуемую раскраску первоначальных $512$ вершин нашего графа.