Г. Челноков

Задача №1. Десятичная запись натурального числа

$N$ составлена только из единиц и двоек. Известно, что вычёркиванием цифр из этого числа можно получить любое из 10000 чисел, состоящих из 9999 единиц и одной двойки. Найдите наименьшее возможное количество цифр в записи числа

$N$ . ( Г. Челноков )
комментарий/решение(1) олимпиада

Задача №2. Найдите наибольшее вещественное

$k$ , для которого существуют множество

$X$ и его подмножества

$Y_1$ ,

$Y_2$ ,

$\dots$ ,

$Y_{31}$ , удовлетворяющие следующим двум условиям:
(1) для любых двух элементов

$X$ найдется подмножество

$Y_i$ , не содержащее ни одного из них;
(2) при любом сопоставлении подмножествам

$Y_i$ неотрицательных чисел

$\alpha_i$ с суммой, равной 1, найдется такой элемент из

$X$ , что сумма

$\alpha_i$ , сопоставленных всем содержащим его подмножествам

$Y_i$ , не меньше

$k$ . ( И. Богданов, Г. Челноков )
комментарий/решение олимпиада

Задача №3. Дано натуральное число

$k$ . В городе несколько детей, они ходят в несколько кружков. Известно, что в каждый кружок ходит не более

$3k$ детей, любой ребёнок ходит ровно в три кружка, и для любых двух детей есть кружок, в которой оба они ходят. Какое наибольшее количество детей может быть в городе? ( И. Богданов, Г. Челноков )
комментарий/решение(1) олимпиада

Задача №4. На плоскости нарисовано 10-этажное 2-дерево: отмечена вершина

$A_1$ , она соединена отрезками с двумя вершинами

$B_1$ и

$B_2$ , каждая из которых соединена отрезками с двумя из четырех вершин

$C_1, C_2, C_3, C_4$ (каждая из вершин

$C_i$ соединена ровно с одной вершиной

$B_j$ ); и так далее вплоть до 512 вершин

$J_1,\dots,J_{512}$ . Каждая вершина

$J_1,\dots,J_{512}$ покрашена в один из двух цветов: голубой или золотой. Рассматриваются всевозможные перестановки

$f$ множества вершин нарисованного дерева, такие что (i) если вершины

$X$ и

$Y$ были соединены отрезком, то вершины

$f(X)$ и

$f(Y)$ также соединены отрезком, и (ii) если вершина

$X$ была покрашена в какой-то цвет, то вершина

$f(X)$ покрашена в тот же цвет. Для какого максимального

$M$ заведомо найдутся хотя бы

$M$ различных рассматриваемых перестановок?

( Г. Челноков )
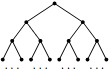
комментарий/решение(1) олимпиада

Задача №5. На плоскость положили несколько синих и зелёных прямоугольных салфеток (возможно, разного размера) с вертикальными и горизонтальными сторонами. Оказалось, что любые две салфетки разного цвета можно пересечь вертикальной или горизонтальной прямой (возможно, по границе). Докажите, что можно выбрать цвет, две горизонтальных прямых и одну вертикальную прямую так, что каждую салфетку выбранного цвета пересекает хотя бы одна из выбранных прямых. ( Г. Челноков )
комментарий/решение(3) олимпиада