қазақша
русскийГ. Челноков
Есеп №1. Натурал $N$ санның ондық жүйедегі жазуы тек «1» және «2» деген цифрлардан құралған. Осы санның цифрларын өшіру арқылы, 9999 «1» және бір «2» цифрларынан құралған 10000 санның кез келгенін алуға болады. $N$ санындағы цифрлар санының ең кіші мүмкін мәнін табыңдар. ( Г. Челноков )
комментарий/решение(1) олимпиада
Есеп №2. Келесі шарттарды қанағаттандыратын, $X$ көпмүшесі мен оның ішкі көпмүшелері ${{Y}_{1}}$, ${{Y}_{2}}$, $\ldots$ ${{Y}_{31}}$ үшін табылатын ең үлкен нақты $k$-ны анықтаңыз:
1) $X$ көпмүшесінің кез-келген екі мүшесі үшін, олардың ешқайсысын қамтымайтын ${{Y}_{i}}$ ішкі көпмүшесі табылады.
2) Қосындысы 1-ге тең, теріс емес ${{\alpha }_{i}}$ сандарын ${{Y}_{i}}$ ішкі көпмүшелерімен кез-келген салыстыруда, $X$ көпмүшесінен, ${{Y}_{i}}$ ішкі көпмүшесінің барлық мүшелерімен салыстырылған ${{\alpha }_{i}}$ сандарының қосындысы $k$ дан кем емес. ( И. Богданов, Г. Челноков )
комментарий/решение олимпиада
Есеп №3. Натурал $k$ саны берілген. Қалада бірнеше бала бар, олар бірнеше үйірмеге қатысады. Әрбір үйірмеге қатысатын балалар саны $3k$-дан аспайды, кез-келген бала дәл үш үйірмеге қатысады, және кез-келген екі бала үшін, сол екеуі де қатысатын үйірме бар. Қалада ең көп дегенде қанша бала болуы мүмкін? ( И. Богданов, Г. Челноков )
комментарий/решение(1) олимпиада
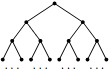
Есеп №4. На плоскости нарисовано 10-этажное 2-дерево: отмечена вершина $A_1$, она соединена отрезками с двумя вершинами $B_1$ и $B_2$, каждая из которых соединена отрезками с двумя из четырех вершин $C_1, C_2, C_3, C_4$ (каждая из вершин $C_i$ соединена ровно с одной вершиной $B_j$); и так далее вплоть до 512 вершин $J_1,\dots,J_{512}$. Каждая вершина $J_1,\dots,J_{512}$ покрашена в один из двух цветов: голубой или золотой. Рассматриваются всевозможные перестановки $f$ множества вершин нарисованного дерева, такие что (i) если вершины $X$ и $Y$ были соединены отрезком, то вершины $f(X)$ и $f(Y)$ также соединены отрезком, и (ii) если вершина $X$ была покрашена в какой-то цвет, то вершина $f(X)$ покрашена в тот же цвет. Для какого максимального $M$ заведомо найдутся хотя бы $M$ различных рассматриваемых перестановок?
комментарий/решение(1) олимпиада
Есеп №5. Түсі жасыл немесе көк болатын, тіктөртбұрыш пішінді бірнеше майлық бар (олардың өлшемдері әртүрлі болуы мүмкін). Олардың әрбірін қабырғалары көлденең және тігінен келетіндей жазықтыққа қойып шыққан. Түрлі түсті кез келген екі майлықты тік немесе көлденең сызықпен (мүмкін, шекара бойымен) қиып өтуге болатыны белгілі. Келесі шартты қанағаттандыратын бір түс таңдап алуға болатынын дәлелдеңіз: екі көлденең және бір тік түзуді таңдауға болады және таңдап алған түстің барлық майлықтарын осы таңдаған үш түзудің кемінде біреуі қияды. ( Г. Челноков )
комментарий/решение(3) олимпиада