1-я олимпиада им. Шалтая Смагулова, 7 класс, 1 тур, 2016 г.
Задача №1. Сколько процентов от $5\%$ от числа $a$ составляет столько же, сколько $8\%$
от $3\%$ от числа $2a$?
комментарий/решение(2)
комментарий/решение(2)
Задача №2. Найдите наименьшее натуральное число, которое нужно добавить к числу 2016, чтобы получился квадрат целого числа.
комментарий/решение(2)
комментарий/решение(2)
Задача №3. Кот в сапогах за один размах лап может порвать один кусок листа бумаги на 5 мелких куска. В начале был один большой кусок. Сколько размахов сделал Кот, если в конце было 25 мелких кусков?
комментарий/решение(2)
комментарий/решение(2)
Задача №4. Сейчас электронные часы показывают время 00:00, то есть 12 часов ровно. Что покажут электронные часы через 1000 минут? (Например, 21:30 означает, что сейчас время пол десятого.)
комментарий/решение(3)
комментарий/решение(3)
Задача №5. Среднее арифметическое шести чисел равно 12. После того, как одно из шести чисел удалили, среднее арифметическое оставшихся пяти чисел оказалось равно 10. Чему было равно удалённое число?
комментарий/решение(6)
комментарий/решение(6)
Задача №6. Количество книг у Петра больше 150, но меньше 200. Из них $20\%$ — романы, а 1/7 — сборники стихов. Сколько книг у Петра?
комментарий/решение(2)
комментарий/решение(2)
Задача №7. Среди кошек, обитающих в лагере «Ласточка», три — пушистые, а две — полосатые. Какое наименьшее количество неполосатых пушистых кошек может быть в лагере?
комментарий/решение(2)
комментарий/решение(2)
Задача №8. В треугольнике $ABC$ угол $A$ в три раза больше угла $B$ и равен половине угла $C$. Чему равен угол $A$?
комментарий/решение(3)
комментарий/решение(3)
Задача №9. Пусть $p$ и $q$ — натуральные числа. Рассмотрим пять чисел: $pq + 2$, $p^2 +q^3$, $(p + 1)(q + 1)$, $(p +q)^2$, $p(q + 1)$. Какое наибольшее количество четных чисел может оказаться в этой пятерке?
комментарий/решение(1)
комментарий/решение(1)
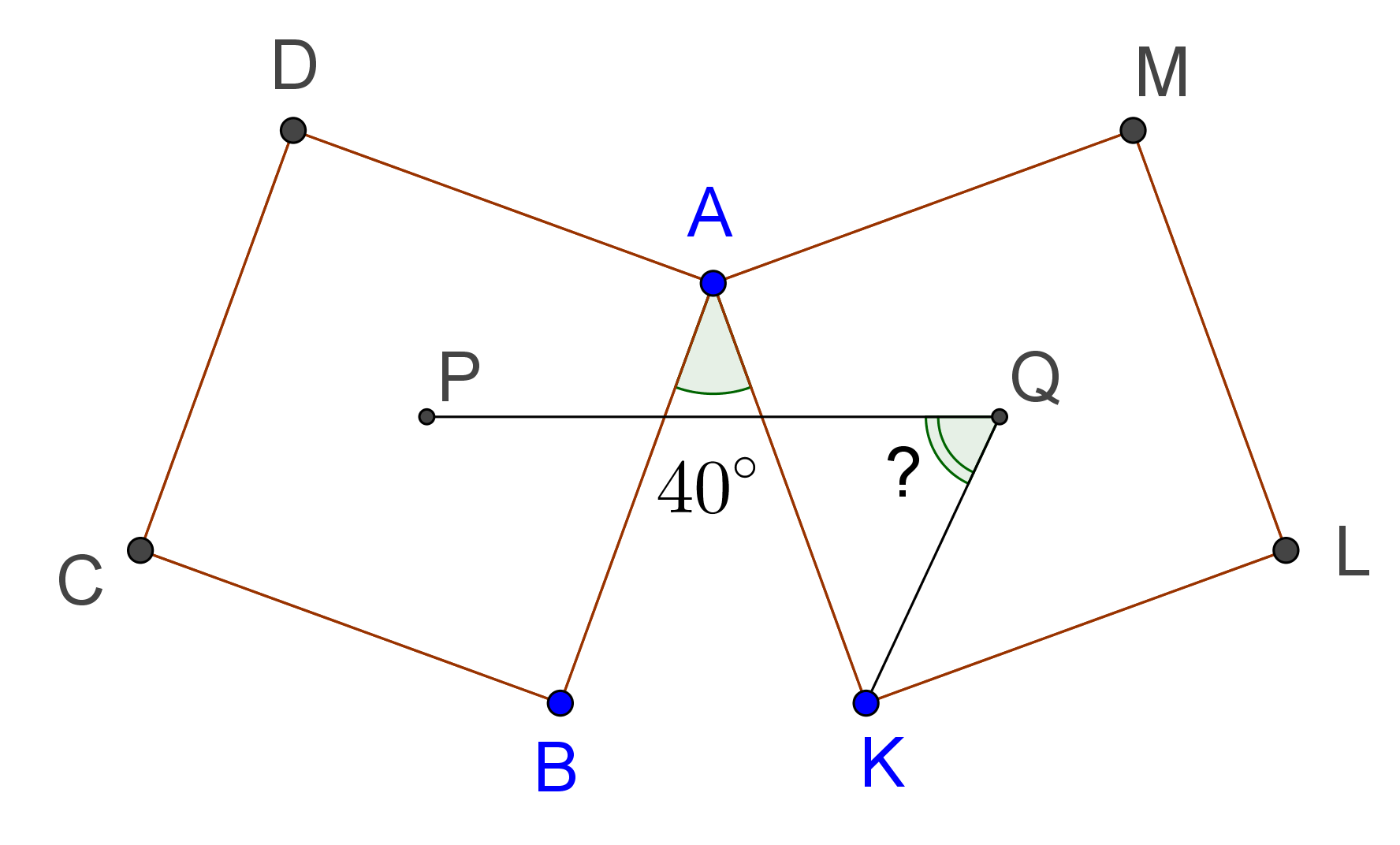
Задача №10. Квадрат $AKLM$ получен поворотом квадрата $ABCD$ вокруг точки $A$ на угол $130^\circ$ против часовой стрелки (см.рис.ниже). $P$ — центр квадрата $ABCD$, $Q$ — центр квадрата $AKLM$. Найдите угол $PQK$.
комментарий/решение(4)
комментарий/решение(4)
Задача №11. Асан выписал все трехзначные числа. А из выписанных чисел Есен стер только те числа, произведение цифр которых равно нулю. Сколько чисел стер Есен?
комментарий/решение(4)
комментарий/решение(4)
Задача №12. Есен выбрал 10 натуральных чисел, и сложил два числа всевозможных пар. Асан заметил, что среди данных полученных 45 сумм, 21 из них нечетны. Известно, что среди выбранных 10 чисел нечетных больше чем четных. Сколько из них нечетных?
комментарий/решение(2)
комментарий/решение(2)
Задача №13. Из набора чисел 1, 2, $\ldots$, 1000 вычеркнуты все четные числа, а также все такие числа $x$, что $1000-x$ делится на 3. Сколько чисел осталось?
комментарий/решение(3)
комментарий/решение(3)
Задача №14. Даны четыре числа. Отношение первого числа ко второму равно 1/7, отношение второго к третьему равно 1/8, третьего к четвертому равно 1/9. Чему равно отношение первого числа к четвертому?
комментарий/решение(1)
комментарий/решение(1)
Задача №16. На плоскости даны 5 горизонтальных и 4 вертикальных прямых. Сколько прямоугольников могли образоваться с помощью этих линий?
комментарий/решение(3)
комментарий/решение(3)
Задача №18. Сколькими способами можно разбить на пары числа 1, 2, 3, 4, 5, 6, 7, 8 так, чтобы разности большего и меньшего чисел во всех парах были одинаковы?
комментарий/решение(1)
комментарий/решение(1)
Задача №19. На какую наибольшую степень числа 2 делится число $6^{2016}-2^{2016}$?
комментарий/решение(8)
комментарий/решение(8)
Задача №20. Вася выписал все числа, произведение цифр которых равно 2016. Вова выбрал наименьшее из них. Какое число выбрал Вова?
комментарий/решение(1)
комментарий/решение(1)