Шалтай Смағұлов атындағы 1-ші олимпиада, 7 сынып, 1 тур, 2016 ж.

Есеп №1. $a$ санының $5\%$-нің қанша проценті $2a$ санының $3\%$-нің $8$ процентіндей болады.
комментарий/решение(2)

Есеп №2. 2016 санына натурал санды қосқанда, қосынды толық квадрат болатындай, қосу керек натурал санның ең кішісін табыңыз.
комментарий/решение(2)

Есеп №3. «Кот в сапогах» қолын бір рет серпігенде, бір қағаз парақ бөлігі 5 кіші бөлікке бөледі. Басында бір үлкен бөлік болған. Ол қолын бірнеше рет серпігеннен кейін, соңында барлығы 25 бөлік болған.«Кот в сапогах» қолын неше рет серпіген?
комментарий/решение(2)

Есеп №4. Қазір электронды сағат 00:00 көрсетіп тұр, яғни дәл 12 сағат. Сол электронды сағат 1000 минуттан кейін не көрсетеді? (Мысалға, 22:30 деген қазір он жарым деген сөз.)
комментарий/решение(3)

Есеп №5. Алты санның арифметикалық ортасы 12-ге тең. Осы сандардың ішінен біреуін алып тастағаннан кейін, қалған бес санның арифметикалық ортасы 10-ға тең болған. Алынып тастаған сан неге тең?
комментарий/решение(6)

Есеп №6. Пётрдің кітаптар саны 150-ден үлкен бірақ 200-ден кіші. Кітаптардың $20\%$-ы — романдар, ал 1/7 бөлігі — өлеңдер жинағы. Пётрда барлығы қанша кітап бар?
комментарий/решение(2)

Есеп №7. «Ласточка» лагерінде мекендейтін мысықтардың үшеуі мамық, екеуі жолақ. Лагерде ең аз дегенде қанша жолақ емес үлпілі мысық болуы мүмкін?
комментарий/решение(2)

Есеп №8. $ABC$ үшбұрышында $A$ бұрышы $B$ бұрышынан үш есе үлкен және $C$ бұрышының жартысына тең. $A$ бұрышы нешеге тең?
комментарий/решение(3)

Есеп №9. $p$ және $q$ — натурал сандар болсын. Келесі бес сандарды қарастырайық: $pq + 2$, ${p^2 +q^3}$, ${(p + 1)(q + 1)}$, ${(p +q)^2}$, ${p(q + 1)}$. Осы сандардың ішінде ең көп дегенде қаншасы жұп бола алады?
комментарий/решение(1)

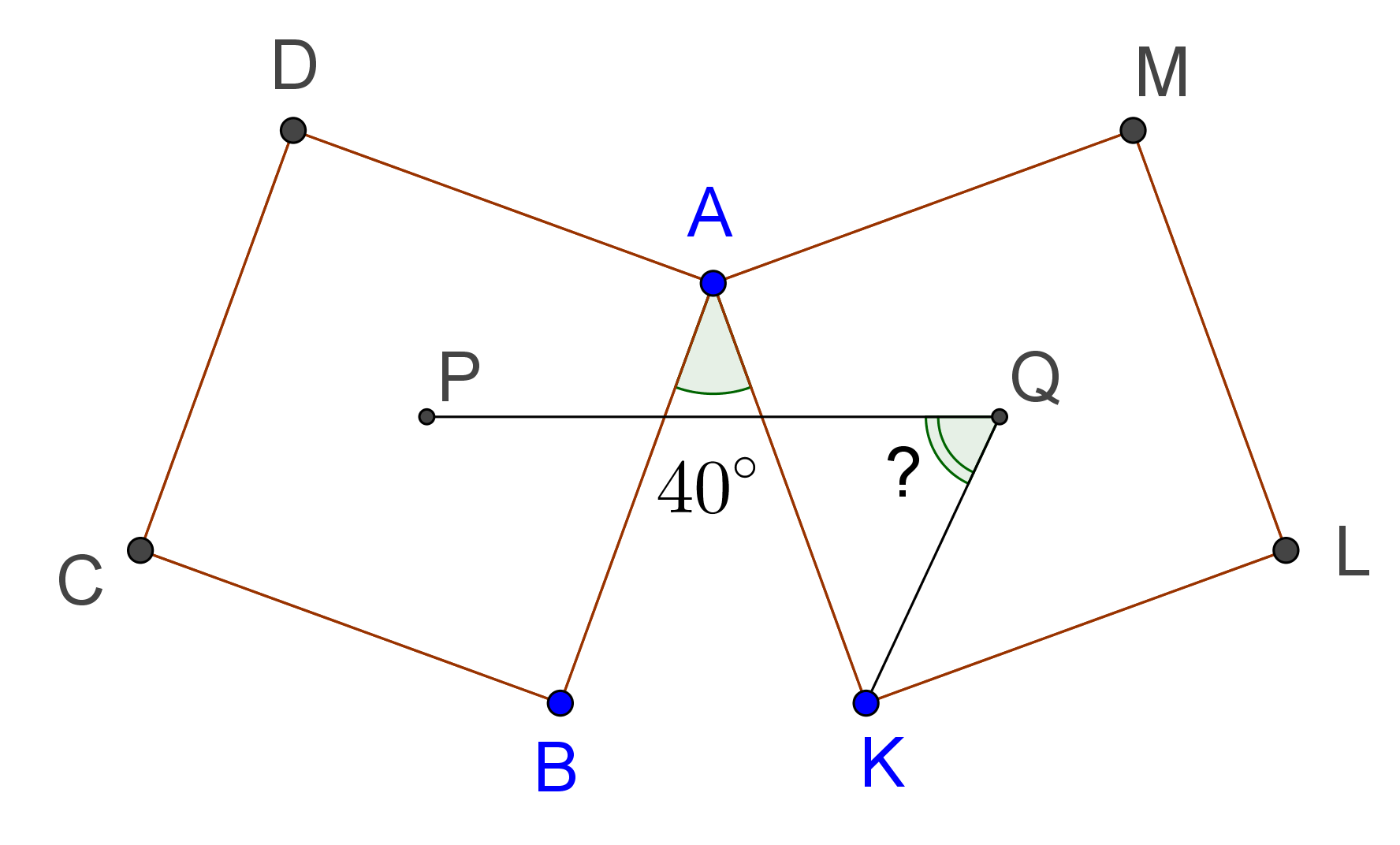
Есеп №10. $ABCD$ квадратын $130^\circ$-ға сағат тіліне қарсы бұрғанда, $AKLM$ квадраты алынған (төмендегі суретті қара). $P$ — $ABCD$ центрі, $Q$ — $AKLM$ центр. $PQK$ бұрышын табыңыз.

комментарий/решение(4)

Есеп №11. Асан барлық үштаңбалы сандарды жазып шықты. Ал Есен осы сандар ішінен тек цифрларының көбейтіндісі ноль болатын сандарды сызып тастады. Есен қанша санды сызды?
комментарий/решение(4)

Есеп №12. Есен 10 натурал санды таңдап алып, кез келген мүмкін болатын жұптардағы сандарды қосты. Асан пайда болған 45 қосындының ішінде 21 қосындының тақ екенін байқаған. Есен таңдаған 10 санның ішінде тақ сандардың саны жұп сандардың санынан көп екені белгілі. Сол 10 санның ішінде қаншасы тақ?
комментарий/решение(2)

Есеп №13. 1, 2, $\ldots$, $1000$ сандар тізімінен барлық жұп сандар сызылды. Және де сол тізімнен $1000-x$ саны 3-ке бөлінетіндей барлық $x$ сандары сызылған. Қанша сан сызылмай қалған?
комментарий/решение(3)

Есеп №14. Төрт сан берілген. Бірінші санның екінші санға қатынасы 1/7-ге тең, екінші санның үшінші санға қатынасы 1/8-ге тең, үшінші санның төртінші санға қатынасы 1/9-ға тең. Бірінші санның төртінші санға қатынасы неге тең?
комментарий/решение(1)

Есеп №15. Уақыт 20:16 болған кезде, тілшелі сағаттың минут тілшесі мен сағат тілшесінің арасындағы бұрыш неге тең?
комментарий/решение(7)

Есеп №16. Жазықтықта 5 көлденеңнен және 4 тігінен келген түзулер берілген. Осы түзулердің көмегімен барлығы қанша тіктөртбұрыш құралуы мүмкін?
комментарий/решение(3)

Есеп №17. Теңдеуді шешіңіз: ${50^{50}}:{25^{25}} = {X^{25}}.$
комментарий/решение(1)

Есеп №18. 1, 2, 3, 4, 5, 6, 7, 8 сандарын келесі шарт орындалатындай қанша әдіспен жұптарға бөлсе болады: кез келген жұп үшін үлкен сан мен кіші санның айырмасы бірдей?
комментарий/решение(1)

Есеп №19. Екінің қандай ең үлекн дәрежесіне $6^{2016}-2^{2016}$ саны бөлінеді?
комментарий/решение(8)

Есеп №20. Вася цифрларының көбейтіндісі 2016 болатын барлық сандарды жазып шыққан. Сол жазылған сандардың ішінен Вова ең кішісін таңдап алды. Вова таңдап алған сан неге тең?
комментарий/решение(1)