7-я олимпиада им. Шалтая Смагулова, 6-7 класс, 3 (командный) тур

Есеп №1. 1-ден 12-ге дейінгі натурал сандарды кез келген екі көрші санның айырмасы 1-ге немесе 2-ге тең болатындай етіп шеңбер бойына орналастырыңыз.
комментарий/решение(1)

Есеп №2. Ребустың бір шешімін табыңыз:

$AL\cdot FA=RABI$ . Мұнда әртүрлі әріптер әртүрлі цифрларды, ал бірдей әріптер бірдей цифрларды білдіреді.
комментарий/решение(2)

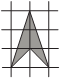
Есеп №3. Суретте көрсетілген фигураны үш бөлікке бөліп, олардан шаршы құрастырыңыз. Бөліктерден шаршыны қалай құрастыру керек екенін көрсетіңіз. Кесулер тор сызықтарымен өтуі міндетті емес.

комментарий/решение(1)

Есеп №4. Сандар тізбегі келесідей құрастырылған: алғашқы үш сан 1, 2, 3 сандары; ал әрбір келесі сан алдыңғы үш санның қосындысының соңғы цифры болып табылады. Бұл қатарда 2, 3, 1 (дәл осы ретпен) үштігі табыла ма?
комментарий/решение(1)

Есеп №5. Оң

$a,b,c$ сандары келесі қасиетке ие:

$a,b,c$ сандарының ешқайсысы бүтін емес, бірақ барлық

$ab,bc,ca,abc$ төрт сан — бүтін сандар.
а) Осы шарттарды қанағаттандыратын

$\left( a,b,c \right)$ үштігіне бір мысал келтіріңіз.
б) Осы шарттарды қанағаттандыратын шексіз көп

$\left( a,b,c \right)$ үштіктері бар екенін дәлелдеңіз.
комментарий/решение(1)

Есеп №6.

$ABC$ үшбұрышында

$C$ бұрышы

$A$ бұрышынан үш есе үлкен.

$AB$ қабырғасында

$BD=BC$ болатындай

$D$ нүктесі белгіленген. Егер

$AD=4$ болса,

$CD$ қабырғасын табыңыз.
комментарий/решение(1)

Есеп №7. Шахмат турнирінде әр екі қатысушы бір-бірімен бір ойын ойнады. Турнир соңында жеңімпаз болған ойыншы барлығын жеңгені, бірақ қалған ойыншылардың жинаған ұпай санынан 5 есе аз ұпай жинағаны белгілі болды. Турнирге неше ойыншы қатысқан? (Шахмат ойынында жеңіс үшін 1 ұпай, тең ойын үшін — 0,5 ұпай, жеңіліс үшін — 0 ұпай алады.)
комментарий/решение(1)

Есеп №8.

${{2}^{a}}$ санының цифрларын орындарымен ауыстыру арқылы

${{2}^{b}}$ санын алуға болатындай

$a$ және

$b$ түрлі натурал сандары табыла ма?
комментарий/решение

Есеп №9.

$n$ санының қандай мәнінде өлшемі

$n\times n$ тақтаны төрт ұяшықтан құралған «Г» тәріздес фигуралармен жауып шыға аламыз?
комментарий/решение

Есеп №10. Екі натурал санның қосындысы 2015-ке тең. Осы екі санның көбейтіндісі ең көп дегенде неше нөлмен аяқтала алады?
комментарий/решение

Есеп №11.

$*+**+***+****=2024$ мысалында дұрыс теңдік шығатындай етіп, жұлдызшаларды 0-ден 9-ға дейінгі (әрқайсысын бір бірден қолданып) цифрларды қойып шығуға бола ма?
комментарий/решение

Есеп №12. Түрлі

$n$ натурал санның көбейтіндісінің кемінде

$\frac{n(n-1)}{2}+1$ бөлгіші бар екенін дәлелдеңіз.
комментарий/решение

Есеп №13. Дөңес

$ABCD$ төртбұрышында

$AB=BC=CD$ және

$\angle ABC+\angle BCD=240^\circ$ теңдіктері орындалады.

$CAD$ бұрышын табыңыз.
комментарий/решение(1)

Есеп №14. Нақты

$a,b,c$ сандары

${{a}^{3}}+{{b}^{3}}+{{c}^{3}}={{a}^{2}}+{{b}^{2}}+{{c}^{2}}=a+b+c=1$ теңдіктерін қанағаттандырады.

$a, b, c$ сандарының арасында 0 саны бар екенін дәлелдеңіз.
комментарий/решение(1)

Есеп №15.

$n^2 < a^3 < b^3 < (n+1)^2$ теңсіздіктері орындалатындай натурал

$a, b, n$ сандары табыла ма?
комментарий/решение(1)

Есеп №16.

$x(x+1)(x+2)(x+3)(x+4)=32\cdot y(y+1)(y+2)(y+3)(y+4)$ теңдігін қанағаттандыратын натурал

$(x,y)$ сандар жұбы табыла ма?
комментарий/решение