7-я олимпиада им. Шалтая Смагулова, 6-7 класс, 3 (командный) тур
Задача №1. Расставьте по кругу натуральные числа от 1 до 12 так, чтобы разность любых двух соседних чисел равнялась 1 или 2.
комментарий/решение(2)
комментарий/решение(2)
Задача №2. Найдите одно решение ребуса: $AL\cdot FA=RABI$. Здесь разные буквы означают разные цифры, а одинаковые буквы — одинаковые цифры.
комментарий/решение(2)
комментарий/решение(2)
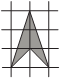
Задача №3. Разрежьте фигуру, изображенную на рисунке, на три части так, чтобы из них можно было сложить квадрат. Покажите, как именно сложить из них квадрат. Разрезы могут идти не по линиям сетки.
комментарий/решение(1)
комментарий/решение(1)
Задача №4. Последовательность чисел строится следующим образом: три первых числа последовательности — числа 1, 2, 3; каждое следующее число — это последняя цифра суммы трех предыдущих чисел. Может ли в этой последовательности встретиться три подряд идущих числа 2, 3, 1 (в указанном порядке)?
комментарий/решение(1)
комментарий/решение(1)
Задача №5. Положительные числа $a,b,c$ обладают следующими условиями: ни одно из чисел $a,b,c$ не является целым, но все четыре числа $ab,bc,ca,abc$ являются целыми.
а) Приведите один пример такой тройки $\left( a,b,c \right)$.
б) Докажите, что таких троек $\left( a,b,c \right)$ бесконечно много.
комментарий/решение(1)
а) Приведите один пример такой тройки $\left( a,b,c \right)$.
б) Докажите, что таких троек $\left( a,b,c \right)$ бесконечно много.
комментарий/решение(1)
Задача №6. В треугольнике $ABC$ угол $C$ в три раза больше угла $A$. На стороне $AB$ взята такая точка $D$, что $BD=BC$. Найдите $C D$, если $A D=4$.
комментарий/решение(1)
комментарий/решение(1)
Задача №7. В шахматном турнире каждый участник сыграл с каждым по одной партии. Победитель выиграл у всех и набрал в 5 раз меньше очков, чем все остальные вместе. Сколько было участников? (За победу в шахматной партии участник получает 1 очко, за ничью — 0,5 очка, за поражение — 0 очков.)
комментарий/решение(1)
комментарий/решение(1)
Задача №8. Существуют ли различные натуральные числа $a$ и $b$ такие, что, переставляя цифры числа ${{2}^{a}}$, можно получить число ${{2}^{b}}$.
комментарий/решение(1)
комментарий/решение(1)
Задача №9. При каких $n$ доску $n\times n$ можно замостить фигурками из четырех клеток формы «Г»?
комментарий/решение(1)
комментарий/решение(1)
Задача №10. Сумма двух натуральных чисел равна 2015. Каким наибольшим числом нулей может оканчиваться их произведение?
комментарий/решение(1)
комментарий/решение(1)
Задача №11. Можно ли в примере $*+**+***+****=2024$ звездочки заменить цифрами от 0 до 9 (каждую цифру используя по одному разу), чтобы равенство было верным?
комментарий/решение(1)
комментарий/решение(1)
Задача №12. Докажите, что произведение $n$ различных натуральных чисел имеет не меньше $\frac{n(n-1)}{2}+1$ делителей.
комментарий/решение
комментарий/решение
Задача №13. В выпуклом четырехугольнике $ABCD$ выполнены равенства $AB=BC=CD$ и $\angle ABC+\angle BCD=240^\circ$. Найдите угол $CAD$.
комментарий/решение(1)
комментарий/решение(1)
Задача №14. Действительные числа $a,b,c$ удовлетворяют равенствам $${{a}^{3}}+{{b}^{3}}+{{c}^{3}}={{a}^{2}}+{{b}^{2}}+{{c}^{2}}=a+b+c=1.$$ Докажите, что среди $a,b,c$ есть число 0.
комментарий/решение(1)
комментарий/решение(1)
Задача №15. Существуют ли натуральные числа $a, b, n$ такие, что $$n^2 < a^3 < b^3 < (n+1)^2?$$
комментарий/решение(1)
комментарий/решение(1)
Задача №16. Существуют ли пары натуральных чисел $(x,y)$ таких, что $$x(x+1)(x+2)(x+3)(x+4)=32\cdot y(y+1)(y+2)(y+3)(y+4)?$$
комментарий/решение
комментарий/решение