Олимпиада Туймаада по математике. Младшая лига. 2004 год
Задача №1. На доске написано положительное рациональное число. Каждую минуту Вася
заменяет написанное на доске число $r$ на $\sqrt{r+1}$. Докажите, что
когда-нибудь он получит иррациональное число.
(
из материалов олимпиад
)
комментарий/решение(1)
комментарий/решение(1)
Задача №2. При каких натуральных $n \geq 3$ числа от 1 до $n$ можно расставить по
кругу так, чтобы каждое число не превосходило 60% суммы двух своих соседей?
(
А. Храбров
)
комментарий/решение
комментарий/решение
Задача №3. Точка $O$ — центр описанной окружности остроугольного треугольника
$ABC$. Некоторая окружность проходит через точки $B$ и $C$ и пересекает
стороны $AB$ и $AC$ треугольника. На ее дуге, лежащей внутри треугольника,
выбраны точки $D$ и $E$ так, что отрезки $BD$ и $CE$ проходят через точку $O$.
Перпендикуляр $DD_1$ к стороне $AB$ и перпендикуляр $EE_1$ к стороне $AC$
пересекаются в точке $M$. Докажите, что точки $A$, $M$ и $O$ лежат на одной
прямой.
(
Ф. Бахарев
)
комментарий/решение(1)
комментарий/решение(1)
Задача №4. Даны непересекающиеся конечные множества натуральных чисел $A$ и $B$,
состоящие из $n$ и $m$ элементов соответственно.
Известно, что каждое натуральное число, принадлежащее $A$ или $B$, удовлетворяет
хотя бы одному из условий $k+17 \in A$, $k-31 \in B$.
Докажите, что $17n=31m$.
(
C.Gonciulea
)
комментарий/решение
комментарий/решение
Задача №5. 50 рыцарей короля Артура сидели за круглым столом. Перед каждым из
них стоял бокал красного или белого вина. Известно, что на столе
стоял хотя бы один бокал красного вина и хотя бы один бокал белого вина.
Король два раза хлопнул в ладоши. После первого хлопка каждый рыцарь, перед
которым стоял бокал красного вина, взял у своего левого соседа его бокал,
а после второго хлопка каждый рыцарь, перед которым стоял бокал
белого вина (и, возможно, что-нибудь еще), передал этот бокал
левому соседу своего левого соседа.
Докажите, что кто-то из рыцарей остался без вина.
(
А. Храбров
)
комментарий/решение
комментарий/решение
Задача №6. Назовем натуральное число хорошим, если сумма обратных величин
всех его натуральных делителей — целая. Докажите, что если
$m$ — хорошее число, а $p > m$ — простое, то число $pm$ не является
хорошим.
(
А. Голованов
)
комментарий/решение
комментарий/решение
Задача №7. Вписанная окружность треугольника $ABC$ касается сторон $AB$ и $BC$ в
точках $P$ и $Q$. Прямая $PQ$ пересекает описанную окружность треугольника
$ABC$ в точках $X$ и $Y$. Найдите $\angle XBY$, если $\angle ABC = 90^\circ$.
(
А. Смирнов
)
комментарий/решение(2)
комментарий/решение(2)
Задача №8. В клетках доски $n \times n$ расставлены нули и единицы.
Во всех клетках левого столбца стоят единицы, и в каждой фигурке вида
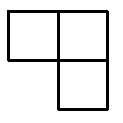 (состоящей из клетки и ее соседей слева и снизу) сумма чисел четна.
Докажите, что в таблице нет двух одинаковых строк.
(состоящей из клетки и ее соседей слева и снизу) сумма чисел четна.
Докажите, что в таблице нет двух одинаковых строк.
комментарий/решение
комментарий/решение