Математикадан «Туймаада» олимпиадасы. Кіші лига. 2004 жыл

Есеп №1. Тақтаға оң рационал сан жазылды. Әр минут сайын Вася, тақтаға жазылған $r$ санын $\sqrt{r+1}$ санына ауыстырып отыр. Бір кезде ол иррационал сан алатынын дәлелдеңіз. ( из материалов олимпиад )
комментарий/решение(1)

Есеп №2. Қандай натурал $n\ge 3$ үшін, 1-ден $n$-ге дейінгі сандарды шеңбер бойымен, әр сан көршілерінің қосындысының 60%-ынан аспайтындай орналастыруға болады? ( А. Храбров )
комментарий/решение

Есеп №3. $O$ нүктесі, $ABC$ үшбұрышына сырттай сызылған үшбұрыштың центрі. Бір шеңбер $B$ және $C$ нүктелері арқылы өтіп $AB$ және $AC$ қабырғаларын қияды. Осы шеңбердің, үшбұрыш ішінде орналасқан доғасының бойынан, $BD$ және $CE$ кесінділері $O$ нүктесі арқылы өтетіндей, $D$ және $E$ нүктелері алынған. $AB$ қабырғасына жүргізілген перпендикуляр $D{{D}_{1}}$ және $AC$ қабырғасына жүргізілген перпендикуляр $E{{E}_{1}}$, $M$ нүктесінде қиылысады. $A$, $M$ және $O$ нүктелері бір түзудің бойында жататынын дәлелдеңіз. ( Ф. Бахарев )
комментарий/решение(1)

Есеп №4. $n$ және $m$ элементтен тұратын, қиылыспайтын шектеулі $A$ және $B$ натурал сандар жиындары берілген. $A$ немесе $B$ жиынына тиесілі әрбір натурал сан келесі шарттардың кем дегенде біреуін орындайды: $k+17\in A$, $k-31\in B$. $17n=31m$ екенін дәлелдеңіз. ( C.Gonciulea )
комментарий/решение

Есеп №5. Дөңгелек үстелде, Артур патшаның 50 серісі отырды. Әрқайсысының алдында ақ немесе қызыл түсті вино құйылған бокал тұрды. Үстелде кем-дегенде бір қызыл түсті және ақ түсті вино құйылған бокал тұрғаны белгілі. Патша екі рет алақанымен қол соқты. Бірінші қол соғудан кейін, алдында қызыл түсті виносы бар сері сол жағындағы көршісінің бокалын өзіне алды, ал екінші қол соғудан кейін, алдында ақ виносы бар сері (басқа да нәрсе болуы мүмкін), осы бокалды сол жағындағы көршісінің сол жағындағы көршісіне берді. Серілердің біреуі виносыз қалғанын дәлелдеңіз. ( А. Храбров )
комментарий/решение

Есеп №6. Санды жақсы деп атайық, егер осы санның бөлгіштерінің кері мәндерінің қосындысы бүтін сан болса. Егер $m$ жақсы сан болса, ал $p > m$ жай сан болса, $pm$ жақсы сан емес екенін дәлелдеңіз. ( А. Голованов )
комментарий/решение

Есеп №7. $ABC$ үшбұрышына іштей сызылған шеңбер, $AB$ және $BC$ қабырғаларымен $P$ және $Q$ нүктелерінде жанасады. $PQ$ түзуі, $ABC$ үшбұрышына сырттай сызылған шеңберді $X$ және $Y$ нүктелерінде қияды. Егер $\angle ABC=90{}^\circ $ болса, $\angle XBY$ бұрышын табыңыз. ( А. Смирнов )
комментарий/решение(2)

Есеп №8. $n\times n$ тақтасының торларына нөлдер және бірлер орналастырылды. Сол жақтағы бағандағы торларда тек бірліктер орналастырылды және әрбір (бір тордан және оның көршілес астындағы немесе сол жағындағы тұратын)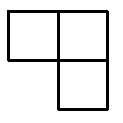

фигурада барлық сандардың қосындысы жұп сан. Кестеде екі бірдей жол жоқ екенін дәлелдеңіз.
комментарий/решение