Городская Жаутыковская олимпиада по математике, 8 класс, 2022 год
Есеп №1. Дөңес $ABCD$ төртбұрышында $M$, $N$, $P$ және $Q$ нүктелері сәйкесінше $AB$, $BC$, $CD$ және $DA$ қабырғаларының орталары. $MP=NQ$ екені белгілі. $AC$ және $BD$ диагоналдарының перпендикуляр екенін дәлелдеңіз.
комментарий/решение(1)
комментарий/решение(1)
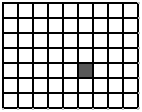
Есеп №2. Өлшемі $9\times 7$ болатын торлы тақта берілген. Тақтада бір клетка белгілеген (суретті қара). Белгіленген клетка ішінде жататын және қабырғалары тор сызықтарында жататын қанша тіктөртбұрыш бар?
комментарий/решение
комментарий/решение
Есеп №3. $x$, $y$, $z$ — оң сандар. Келесі теңсіздікті дәлелдеңіз: $$x^2+xy^2+xyz^2 \ge 4xyz-4.$$
комментарий/решение(3)
комментарий/решение(3)
Есеп №4. $a_1$, $a_2$, $\ldots$, $a_n$ сандары 1, 2, $\ldots$, $n$ сандарының қандай да бір орын ауыстырылымы. Қандай натурал $n$ сандары үшін, $$0, \ a_1,\ a_1 + a_2, \ \ldots, \ a_1 +a_2+ a_3+\ldots +a_n$$ сандарын $n+1$ санына бөлгенде, пайда болған қалдықтар әртүрлі бола алады?
комментарий/решение
комментарий/решение
Есеп №5. Дөңес $PQRS$ төртбұрышында келесі қабырға ұзындықтары берілген: $PQ=40$, $PS=60$ және $RS=20$. Егер $\angle QPS=\angle RSP=60{}^\circ$ болса, онда $QRS$ бұрышы неше градусқа тең?
комментарий/решение(1)
комментарий/решение(1)
Есеп №6. Натурал санның «әр түрлі жай бөлгіштерінің жиыны» деп, оның қайталанбай алынған барлық жай бөлгіштерін айтамыз. Мысалы, 40 санының «әр түрлі жай бөлгіштерінің жиыны» ол 2 және 5 сандары. Екі $A=2^k-2$ және $B=2^k \cdot A$ сандары берілген, бұл жерде $k \ge 2$. $A+1$ және $B+1$ сандарының «әт түрлі жай бөлгіштерінің жиыны» бірдей екенін дәлелдеңіз.
комментарий/решение(1)
комментарий/решение(1)
Есеп №7. Келесі жүйені қанағаттандыратын барлық $(x, y, z)$ нақты сандар үштіктерін табыңыз: \[\left\{ \begin{array}{l} xy = z - x - y,\\ xz = y - x - z,\\ yz = x - y - z. \end{array} \right.\]
комментарий/решение(1)
комментарий/решение(1)
Есеп №8. $M=\{1, 2, \ldots, 9\}$ жиыны берілген. $M$-нің ішкі $S$ жиыны келесі қасиетке ие: $S$-тің қос-қостан алған кез келген екі элементтерінің қосындылары әртүрлі. Мысалы, $S$ ретінде $\{1, 2, 3, 5\}$ жиынын алса болады, ал $\{1,2,3,4,5\}$ жиынын алуға болмайды (өйткені $1+4=2+3$). $S$ жиынында ең көп дегенде қанша элемент болуы мүмкін? Кез келген жиында бірдей сандар болмауы керек екенін еске саламыз.
комментарий/решение(1)
комментарий/решение(1)