Городская Жаутыковская олимпиада по математике, 8 класс, 2022 год

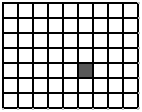
Дана сетчатая таблица $9\times 7$, в которой одна клетка закрашена (см. рис.). Сколько прямоугольников, стороны которого идут по линиям сетки, содержат эту закрашенную клетку?

Комментарий/решение

Мы знаем что в это множество входит сама клетка, будет от нее отталкиваться, продлим стороны клетки, заметим что все прямоугольники которые имеют эту клетку это как раз эта клетка, у которых передвинуты свои стороны в соответственные стороны , поэтому верхний грань мы может двигать с 5 способов, левую 6, правую 4, нижнюю 3, получаем что кол-о таких расположений прямых это 6*5*4*3=360

Ответ : 360

(Примечание : кто не понял что означает стороны в соответственные стороны, например если мы подвинем верхнюю грань на один верх, то получим доминшку 1х2 с черной нижней клеткой, если еще подвинем правую на 2, то получил 3х2 прямоугольник с черной клеткой в нижней левом углу)