Юниорская олимпиада по математике. Областной этап. 2019-2020 учебный год. 8 класс.
Задача №1. В стране 15 городов, некоторые из них соединены авиалиниями, принадлежащими трём авиакомпаниям. Известно, что даже, если любая из авиакомпаний прекратит полёты, можно будет добраться из любого города в любой другой (возможно с пересадками), пользуясь рейсами оставшихся двух компаний, тогда наименьшее количество авиалиний в стране равно
A) 19 B) 20 C) 21 D) 22 E) 25
комментарий/решение
A) 19 B) 20 C) 21 D) 22 E) 25
комментарий/решение
Задача №2. В классе 28 человек. Каждая девочка дружит с 4-мя мальчиками, а каждый мальчик — с 3-мя девочками. Сколько в классе мальчиков и девочек?
A) 16 и 12 B) 20 и 18 C) 15 и 12 D) 20 и 16 E) 26 и 14
комментарий/решение(1)
A) 16 и 12 B) 20 и 18 C) 15 и 12 D) 20 и 16 E) 26 и 14
комментарий/решение(1)
Задача №3. В магазине продаются три вида шоколадок: «Алёнка», «Pierre Markolini», «Noka Vintages Collection». Ерлан задумался: «Сколькими способами он может купить 9 шоколадок»?
A) 50 B) 52 C) 55 D) 105 E) 125
комментарий/решение(1)
A) 50 B) 52 C) 55 D) 105 E) 125
комментарий/решение(1)
Задача №4. Решением уравнения $x\left ( x-1 \right) \left ( x-2 \right) \cdot \ldots \cdot 2\cdot 1={{y}^{2}}-12$ в натуральных числах является пара чисел
A) $(5; 7)$ B) $(4; 6)$ C) $(3; 5)$ D) $(2; 4)$ E) $(6; 8)$
комментарий/решение(1)
A) $(5; 7)$ B) $(4; 6)$ C) $(3; 5)$ D) $(2; 4)$ E) $(6; 8)$
комментарий/решение(1)
Задача №5. Остаток от деления числа ${{1532}^{5}}-1$ на 9 равен
A) 1 B) 2 C) 3 D) 4 E) 5
комментарий/решение(3)
A) 1 B) 2 C) 3 D) 4 E) 5
комментарий/решение(3)
Задача №6. Пятизначное число, являющееся точным квадратом, записывается при помощи цифр 0; 1; 2; 2; 2. Найдите пятизначное число.
A) 22210 B) 22201 C) 22021 D) 20221;
комментарий/решение(1)
A) 22210 B) 22201 C) 22021 D) 20221;
комментарий/решение(1)
Задача №7. Целая часть числа $x$ обозначается символом $[x]$. Например: $x=2, 17$, тогда $[x]=2$. Решите уравнение $[x+2,6]=-7$.
A) $-9\le x<-8$ B) $-9, 6\le x<-4, 4$ C) $-9, 6\le x<-8, 6$ D) $-9, 2\le x<-8, 4$
комментарий/решение(1)
A) $-9\le x<-8$ B) $-9, 6\le x<-4, 4$ C) $-9, 6\le x<-8, 6$ D) $-9, 2\le x<-8, 4$
комментарий/решение(1)
Задача №8. Девочек в математическом кружке меньше $50\%$, но больше $40\%$, тогда наименьшее число участников в математическом кружке равно
A) 5 B) 6 C) 10 D) 7
комментарий/решение
A) 5 B) 6 C) 10 D) 7
комментарий/решение
Задача №9. Арман написал на доске 5 целых чисел. Сложив их попарно, получил следующие 10 чисел: 0, 2, 4, 4, 6, 8, 9, 11, 13, 15. Какое наибольшее число Арман написал на доске?
A) 12 B) 10 C) 15 D) 13
комментарий/решение
A) 12 B) 10 C) 15 D) 13
комментарий/решение
Задача №10. Чтобы узнать, является ли число 1601 простым, его стали последовательно делить на 2, 3, 5 и т. д. На каком простом числе можно прекратить испытания?
A) 31 B) 37 C) 41 D) 43
комментарий/решение(5)
A) 31 B) 37 C) 41 D) 43
комментарий/решение(5)
Задача №11. Фонтан на площади города связан с часами на башне: он работает, когда хотя бы одна из стрелок часов находится между цифрами 3 и 4 или между цифрами 8 и 9. Сколько времени в течении суток этот фонтан работает?
A) 4 ч 20 мин B) 6 ч 20 мин C) 7 ч 20 мин D) 5 ч 30 мин
комментарий/решение
A) 4 ч 20 мин B) 6 ч 20 мин C) 7 ч 20 мин D) 5 ч 30 мин
комментарий/решение
Задача №12. Ажар, Асель, Лена и Камила умеют играть на разных инструментах (рояле, виолончели, гитаре, скрипке), но каждая только на одном. Они же знают иностранные языки (английский, французский, немецкий и китайский), но каждая только один. Известно, что девушка, которая играет на гитаре, говорит по-китайски. Асель не играет ни на скрипке, ни на виолончели и не знает английский язык. Ажар не играет ни на скрипке, ни на виолончели и не знает ни немецкого, ни английского. Девушка, которая говорит по-немецки, не играет на виолончели. Лена знает французский, но не играет на скрипке. На каком инструменте играет Камила, и какой язык она знает? B) скрипка и английский B) скрипка и французский C) гитара и английский D) рояль и китайский
комментарий/решение(1)
комментарий/решение(1)
Задача №13. Какой из перечисленных ниже графов соответствует многограннику, изображённому на рисунке?
A) 1 B) 2 C) 3 D) 4
комментарий/решение

A) 1 B) 2 C) 3 D) 4
комментарий/решение
Задача №14. Разместите восемь козлят и девять гусей в пяти хлевах так, чтобы в каждом хлеве были и козлята и гуси, а число их ног равнялось 10.
A) в 2-х хлевах по 1 козлёнку и 3-м гусям и в 3-х хлевах по 2 козлёнка и 1 гусю B) в 2-х хлевах по 2 козлёнка и 2-м гусям и в 3-х хлевах по 1 козлёнка и 2 гуся C) в 2-х хлевах по 1 козлёнку и 4-м гусям и в 3-х хлевах по 2 козлёнка и 1 гусю D) в 2-х хлевах по 2 козлёнку и 1 гусю и в 3-х хлевах по 1 козлёнка и 2 гуся
комментарий/решение
A) в 2-х хлевах по 1 козлёнку и 3-м гусям и в 3-х хлевах по 2 козлёнка и 1 гусю B) в 2-х хлевах по 2 козлёнка и 2-м гусям и в 3-х хлевах по 1 козлёнка и 2 гуся C) в 2-х хлевах по 1 козлёнку и 4-м гусям и в 3-х хлевах по 2 козлёнка и 1 гусю D) в 2-х хлевах по 2 козлёнку и 1 гусю и в 3-х хлевах по 1 козлёнка и 2 гуся
комментарий/решение
Задача №15. Путешественник посетил деревню, каждый житель которой либо говорит правду, либо всегда лжёт. Все жители деревни встали по кругу лицом к центру, и каждый сказал путешественнику про соседа справа, правдив ли тот. На основании этих сообщений путешественник смог однозначно определить, какую долю от всех жителей составляют лжецы.
A) $60\%$ B) $55\%$ C) $50\%$ D) $45\%$
комментарий/решение
A) $60\%$ B) $55\%$ C) $50\%$ D) $45\%$
комментарий/решение
Задача №16. Квадрат разбит прямыми на 25 одинаковых квадратиков — клеток. В некоторых клетках нарисована одна из диагоналей так, что никакие две нарисованные диагонали не имеют общей точки (даже общего конца). Каково наибольшее возможное число нарисованных диагоналей?
A) 16 B) 17 C) 18 D) 15
комментарий/решение
A) 16 B) 17 C) 18 D) 15
комментарий/решение
Задача №17. Для каждого трёхзначного числа берём произведение его цифр, а затем эти произведения, вычисленные для всех трёхзначных чисел, складываем. В результате получилась сумма
A) 91125 B) 90125 C) 2025 D) 18225
комментарий/решение
A) 91125 B) 90125 C) 2025 D) 18225
комментарий/решение
Задача №18. На полоске $1\times N$ на 25 левых полях стоят 25 шашек. Шашка может ходить на соседнюю справа свободную клетку или перепрыгивать через соседнюю справа шашку на следующую за ней клетку (если эта клетка свободна), движение влево не разрешается. При каком наименьшем $N$ все шашки можно поставить без пробелов в обратном порядке?
A) 45 B) 50 C) 51 D) 49
комментарий/решение
A) 45 B) 50 C) 51 D) 49
комментарий/решение
Задача №19. Число 7 возведено в 19-ю степень. Полученное число вновь возвели 19-ю степень и т. д. Возведение повторили 2020 раз. Определите последнюю цифру полученного числа
A) 7 B) 9 C) 3 D) 1
комментарий/решение(1)
A) 7 B) 9 C) 3 D) 1
комментарий/решение(1)
Задача №20. Прямоугольник составлен из шести квадратов, как показано на рисунке. Найдите сторону самого большого квадрата, если сторона самого маленького квадрата равна 1.
A) 5 B) 6 C) 8 D) 7
комментарий/решение(1)
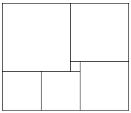
A) 5 B) 6 C) 8 D) 7
комментарий/решение(1)
Задача №21. В 100 г раствора имеется $1\%$ соли. После испарения в растворе стало $2\%$ соли. Сколько весит этот $2\%$-ный раствор соли?
A) 45 г B) 50 г C) 60 г D) 55 г
комментарий/решение(1)
A) 45 г B) 50 г C) 60 г D) 55 г
комментарий/решение(1)
Задача №22. В $\triangle KNM$ $\angle N={{90}^\circ}$, $\angle M={{35}^\circ}$, $\angle PKS={{10}^\circ}$, $\angle SNP={{20}^\circ}$. Найти $\angle PSM$.
A) ${{40}^\circ}$ B) ${{45}^\circ}$ C) ${{60}^\circ}$ D) ${{55}^\circ}$
комментарий/решение(1)
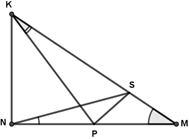
A) ${{40}^\circ}$ B) ${{45}^\circ}$ C) ${{60}^\circ}$ D) ${{55}^\circ}$
комментарий/решение(1)
Задача №23. Какой из графиков соответствует уравнению $\left| y \right|\cdot y=\frac{\left| x \right|}{x}$
A) 1 B) 2 C) 3 D) 4
комментарий/решение(1)
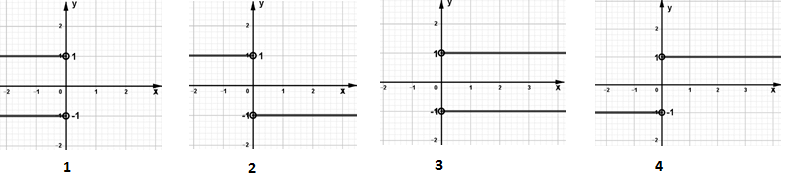
A) 1 B) 2 C) 3 D) 4
комментарий/решение(1)
Задача №24. Архипелаг состоит из нескольких малых островов и одного большого. Было решено построить мосты между островами так, чтобы большой остров соединялся с каждым малым островом двумя мостами, а любые два малых острова были соединены одним мостом. К 1 ноября были построены все мосты между малыми островами и несколько (не менее одного) мостов, ведущих на большой остров, — всего 28 мостов. Сколько всего островов в архипелаге?
A) 9 B) 5 C) 7 D) 8
комментарий/решение
A) 9 B) 5 C) 7 D) 8
комментарий/решение
Задача №25. Найдите наибольшее количество белых доминошек, которое можно вырезать из доски, изображённой на рисунке. Доминошка — это прямоугольник $1 \times 2$.
A) 14 B) 15 C) 16 D) 18
комментарий/решение(3)

A) 14 B) 15 C) 16 D) 18
комментарий/решение(3)
Задача №26. Угол между часовой и минутной стрелкой в 9 часов 10 минут равен
A) ${{140}^\circ}$ B) ${{145}^\circ}$ C) ${{150}^\circ}$ D) ${{155}^\circ}$
комментарий/решение(2)
A) ${{140}^\circ}$ B) ${{145}^\circ}$ C) ${{150}^\circ}$ D) ${{155}^\circ}$
комментарий/решение(2)
Задача №27. В ряд выписано 11 чисел так, что сумма любых трёх идущих подряд чисел равна 18. При этом сумма всех чисел равна 64. Найдите центральное число.
A) 24 B) 12 C) 16 D) 8
комментарий/решение(1)
A) 24 B) 12 C) 16 D) 8
комментарий/решение(1)
Задача №28. На уроке физкультуры весь класс выстроился по росту (у всех детей разный рост). Дамир заметил, что людей, которые выше него, в четыре раза больше, чем людей, которые ниже него. А Ерлан заметил, что людей, которые выше него, в три раза меньше, чем людей, которые ниже него. Сколько всего человек в классе, если известно, что их не больше 30?
A) 24 B) 20 C) 21 D) 27
комментарий/решение(2)
A) 24 B) 20 C) 21 D) 27
комментарий/решение(2)
Задача №29. На одной грани игрального кубика нарисована одна точка, на другой грани — две, на третьей — три, и т. д. Четыре одинаковых игральных кубика сложены так, как показано на рисунке. Сколько в общей сложности точек находится на 6 гранях, которыми касаются кубики?
A) 40 B) 20 C) 24 D) 36
комментарий/решение
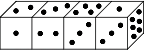
A) 40 B) 20 C) 24 D) 36
комментарий/решение
Задача №30. Денис загадал четыре различных натуральных числа. Он утверждает, что произведение наименьшего и наибольшего чисел равно 32 произведение двух оставшихся чисел равно 14. Чему равна сумма всех четырёх чисел?
A) 42 B) 40 C) 35 D) 45
комментарий/решение(2)
A) 42 B) 40 C) 35 D) 45
комментарий/решение(2)