Юниорская олимпиада по математике. Областной этап. 2019-2020 учебный год. 8 класс.

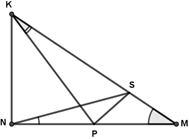
В $\triangle KNM$ $\angle N={{90}^\circ}$, $\angle M={{35}^\circ}$, $\angle PKS={{10}^\circ}$, $\angle SNP={{20}^\circ}$. Найти $\angle PSM$.

   A) ${{40}^\circ}$ B) ${{45}^\circ}$ C) ${{60}^\circ}$ D) ${{55}^\circ}$

Комментарий/решение

Решение:

Так как $\angle K+\angle M=\angle 90$, угол $\angle PKN=\angle 45$

Значит ,$\angle KNS=\angle 70$, $\angle KDN=\angle SDP=\angle 65$ D-это точка пересечения $KP$ и $SN$.

Тогда,$\angle KDS=\angle NDP=\angle 115, а \angle KPN=\angle 45$, а $\angle KSN=\angle 55$.

И мы здесь легко по углам находим что $NK=NP=NS$.

А значит $\triangle SNP$ - равнобедренный.

Тогда $\angle NPS=\angle NSP=\angle 80 \Rightarrow \angle KPS=\angle 35$

Мы находим что $\angle SPM=\angle 100$, значит что $\angle PSM=\angle 45$.

Ответ:$В)45^\circ$