Temirlan Satylkhanov

Есеп №1. (Темірлан vs Рамазан) Тақтада $N$ бүтін сан жазылған. Темірлан және Рамазан келесі ойынды ойнап жатыр:

Олар кезектесіп жүреді, бірінші болып Темірлан жүреді.
Әр жүрісте ойыншы тақтадан кез-келген бастапқы сандарды немесе соңғы сандарды өшіріп тастайды, және кем дегенде бір санды өшіру керек. Бірақ барлық санды өшіріп тастауға болмайды.
Тақтада соңғы сан қалғанда ойын аяқталады. Темірлан сол санның барынша кішкентай болғаның қалайды, ал Рамазан барынша үлкен болғаның қалайды.

Темірлан сыртқа шығып кеткенде, Рамазан тақтадғы $K$ санды өшіріп тастағысы келеді. Ол кез келген сандарды өшіріп тастай алады. Темірлан қайтып келгенде, олар ойынды ойнап бастайды, бірақ тақтада $N-K$ сан жазылып тұрады.
Әрбір $Q$ сан $K_1,K_2, ..., K_Q$ үшін, Рамазан ойында қалған соңғы санның мәнің білгісі келеді, егер ол ойынның басында $K_i$ санды өшіріп тастаса, және екі ойыншыда өзіне қолайлы ойнаса?

Кіріс деректер форматы:

Бірінші жолда бір бүтін сан $N$ берілген.
Екінші жолда $N$ бүтін сан берілген $A_1,A_2,...,A_N (1 \le A_i \le 10^6)$ --- тақтада жазылған сандар.
Үшінші жолда бір бүтін сан $Q$ берілген.
Төртінші жолда $Q$ бүтін сан берілген $K_1,K_2,...,K_Q(0 \le K_i \le N - 1)$.

Шығыс деректер форматы:

Пробел арқылы $Q$ сан шығарыңыз, $i$-ші сан, ол соңғы қалған санның мәні, егер Рамазан алдын ала $K_i$ санды өшіріп тастаса.

Мысалдар:

1.Мысал:

Жауап:

1 3 3 4

2.Мысал:

Жауап:

5 5 5

3.Мысал:

6
2 7 5 4 8 10
3
3 5 2

Жауап:

7 10 7

Түсініктеме:

Бірінші тестте $K=3$ болғанда, Рамазанға бірінші,екінші және төртінші санды өшірген тиімді.

Бағалау:

Есеп 50 тесттен тұрады, әр тест 2 ұпаіға бағаланады.
Тесттердегі шектеулер:

3 тест: Алғашқы үш тест мысалда берілген тесттер
5 тест: $1 \le N \le 3, Q = 1, K_1 = 0$
10 тестте: $1 \le N \le 100, Q = 1, K_1 = 0$
12 тестте: $1 \le N \le 10^5, 1\le Q \le 2, 0 \le K_i \le 1$
10 тестте: $1 \le N \le 10^5, 1 \le Q \le 10^5,0 \le K_i \le N - 1$
10 тестте: $1 \le N \le 10^6, 1 \le Q \le 10^6, 0 \le K_i \le N - 1$

( Temirlan Satylkhanov )
комментарий/решение(14) олимпиада

Есеп №2. (Темірлан vs Рамазан) Тақтада $N$ бүтін сан жазылған. Темірлан және Рамазан келесі ойынды ойнап жатыр:

Олар кезектесіп жүреді, бірінші болып Темірлан жүреді.
Әр жүрісте ойыншы тақтадан кез-келген бастапқы сандарды немесе соңғы сандарды өшіріп тастайды, және кем дегенде бір санды өшіру керек. Бірақ барлық санды өшіріп тастауға болмайды.
Тақтада соңғы сан қалғанда ойын аяқталады. Темірлан сол санның барынша кішкентай болғаның қалайды, ал Рамазан барынша үлкен болғаның қалайды.

Кіріс деректер форматы:

Шығыс деректер форматы:

Мысалдар:

1.Мысал:

Жауап:

1 3 3 4

2.Мысал:

Жауап:

5 5 5

3.Мысал:

6
2 7 5 4 8 10
3
3 5 2

Жауап:

7 10 7

Түсініктеме:

Бірінші тестте $K=3$ болғанда, Рамазанға бірінші,екінші және төртінші санды өшірген тиімді.

Бағалау:

Есеп 50 тесттен тұрады, әр тест 2 ұпаіға бағаланады.
Тесттердегі шектеулер:

3 тест: Алғашқы үш тест мысалда берілген тесттер
5 тест: $1 \le N \le 3, Q = 1, K_1 = 0$
10 тестте: $1 \le N \le 100, Q = 1, K_1 = 0$
12 тестте: $1 \le N \le 10^5, 1\le Q \le 2, 0 \le K_i \le 1$
10 тестте: $1 \le N \le 10^5, 1 \le Q \le 10^5,0 \le K_i \le N - 1$
10 тестте: $1 \le N \le 10^6, 1 \le Q \le 10^6, 0 \le K_i \le N - 1$

( Temirlan Satylkhanov )
комментарий/решение(14) олимпиада

Есеп №3. (Na2a және теңдеу)

Ограничение по времени:

1 second

Ограничение по памяти:

256 megabytes

Na2a информатика сабағында көп қылжағандықтан, мұғалім оған осы тапсырманы берді. Берілген $a_1,...,a_n,S$ сандары үшін, ($a_1 \oplus x) + (a_2 \oplus x) + ... + (a_n \oplus x) = S$ болатындай оң $x$ санын табу керек. Бұл жерде $\oplus$ операциясы биттік XOR немесе жоюшы НЕМЕСЕ. Бұл операция барлық заманауи бағдарламалау тілдерінде бар, С++ және Java тілінде <<$\string^$>>, ал Pascal тілінде <>. Na2a-ға осы есепті шығаруға көмектесіңіз.

Формат входного файла

Бірінші жолда екі бүтін сан $n$ — берілетін сан тезбегінің санды, және $S (1 \le n \le 10^5, 0 \le S \le 10^{12})$ — берілген қосынды. Екінші жолда $n$ бүтін сан: $a_1$, $a_2$, ..., $a_n(0 \le a_i \le 10^{12})$ берілген.

Формат выходного файла

Егер теңдеудің жауабы жоқ болған жағдайда -$1$ шығарыңыз. Басқа жағдайда теңдеу шешілетін $x(x \ge 0)$ санын шығарыңыз. Бірнеше жауап болған жағдайда, кез келген жауап шығаруға болады.

Система оценки

Есеп бес бөлімнен тұрады, әр бөлімде есептің берілгеніндегі шарттар орындалады және:

$n \le 1000, a_i,s \le 1000$. Бөлім $7$ ұпайға бағаланады.
$n = 2, a_i,s \le 10^{12}$. Бөлім $22$ ұпайға бағаланады.
$n \le 10^4, a_i,s \le 10^6$. Бөлім $20$ ұпайға бағаланады.
$n \le 10^5, a_i,s \le 5 \cdot 10^7$. Бөлім $16$ ұпайға бағаланады.
$n \le 10^5, a_i,s \le 10^{12}$. Бөлім $35$ ұпайға бағаланады.

Пример:

Вход

3 4
1 2 3

Ответ

\Note Аралас НЕМЕСЕ операциясы төмендегі ақиқаттық кестесіне сәйкес операндтардың (сандардың) қосындысын анықтайды.\\ 1 $xor$ 1 = 1, 1 $xor$ 0 = 1\\ 0 $xor$ 1 = 1, 0 $xor$ 0 = 0\\ Операндтар ондық түрде жазылады, бірақ орындалғанда олар екілік түрге түрлендіріледі. Нәтижесі ондық түрде көрсетіледі. Мысалға, егер $X$ = $109_{10}$ = $1101101_{2}$, $Y$ = $41_{10}$ = $101001_{2}$ сонда: $X$ $\oplus$ $Y$ = $68_{10}$ = $1000100_{2}$. ( Temirlan Satylkhanov )
комментарий/решение(2) олимпиада

Есеп №4. (Тиманың бапкерлік таңдауы)

Ограничение по времени:

4 seconds

Ограничение по памяти:

256 megabytes

Жақын уақыттан бері Тима баскетбол командасын жаттықтыруды бастады. Команданың капитаны ретінде әрқашан бойы ең ұзын ойыншы таңдалады. Ол команданың сәйкес келмеушілік формуласын ойлап тапты. Команданың сәйкес келмеушілігі оның капитатының бойымен қалғандарының бойының айырмаларының қосындысы. Анықтап айтсақ, $h_1, h_2, ... , h_m$ — командадағы ойыншылардың бойларының ұзындығы болсын, $mx = max(h_1, h_2, ..., h_m)$, онда сәйкес келмеушілік = $\sum_{i=1}^{m} mx$-$h_i$. Тимада бір ретте тұрған $n$ ойыншы бар, $i$-ші ойыншының бойы $a_i$. Ол барлық ойыншыны $k$ командаға бөлгісі келеді, әр ойыншы бір командада болу керек және әр команда ретте қатар тұрған ойыншылардан құралуы керек. Тима барлық команданың сәйкес келмеушіліктерінің қосынды аз болатындай бөлгісі келеді. Тимаға командаларды қолайлы бөлуге көмектесіңіз.

Формат входного файла

Бірінші жолда екі бүтін сан берілген $n$ және $k$ ($1 \le n \le 10^5$, $1 \le k \le min(n, 20)$) — ойыншылардың саны және командалардың саны. Екінші жолда $n$ бүтін $a_i$ ($1 \le a_i \le 10^6$) — қатардың сол жағынан $i$-ші тұрған ойыншының бойының ұзындығы.

Формат выходного файла

Жалғыз бүтін сан шығарыңыз — есептің жауабын.

Система оценки

Есеп алты бөлімнен тұрады, әр бөлімде есептің берілгендегі шарртар орындалады және:

$n \le 100$, $k = 1$. Бөлім $5$ ұпайға бағаланады.
$n \le 2000$. Бөлім $11$ ұпайға бағаланады.
$k = 2$. Бөлім $8$ ұпайға бағаланады.
$k = 3$. Бөлім $15$ ұпайға бағаланады.
$a_i \le a_{i+1}$, барлық $1 \le i < n$ үшін. Бөлім $19$ ұпайға бағаланады.
Есептің еңгізу форматындағы шарттар орындалады. Бөлім $42$ ұпайға бағаланады.

Пример:

s Вход

7 3
6 4 1 5 3 2 2

Ответ

Вход

5 2
4 1 5 5 6

Ответ

Вход

9 2
3 7 4 1 3 2 4 6 7

Ответ

( Temirlan Satylkhanov )
комментарий/решение олимпиада

Есеп №5. (Алмалар)

Ограничение по времени:

1 second

Ограничение по памяти:

64 megabytes

Тима жәңе оның $N - 1$ достары алма жинады. Оларды $1$—ден $N$—ге дейінгі сандармен нөмірлейміз. Тиманың нөмері $1$. Тима өзіндегі алмалар саны қалғандарынан көп екенің байқап, оларға өз алмасымен бөлісетін болды. Ол кімде қанша алма бар, оған соншама алма берді. Мысалы, біреуде $X$ алма болса, Тима оған $X$ алма берді. Одан кейін нөмірі $2$—ші адам кімде қанша алма бар, соған сонша алма берді. Осылай $N$-ші адамға дейін жасады. Соныңда барлығында бірдей алма саны болды. Тима бастапқысында кімде қанша алма болғаның білгісі келеді. Ол басында өзінде $A_1$ алма болғанын біледі.

Формат входного файла

Бірінші жолда бір бүтін сан берілген $T(1\le T \le 1000)$ — тесттер саны. Келесі $T$ жолда екі бүтін саннан жазылған $N$ ($1 \le N \le 50$),$1\le A_1\le 10^{16}$.

Формат выходного файла

$T$ — жол шығарыңыз, егер мұндай жағдай мүмкін емес болса $-1$ шығарыңыз. Олай болмаса $N$ бүтін $A_1,A_2, .., A_N$ сандарың шығарыңыз. Егер есептің бірнеше жауабы болса, кез келгенін шығарыңыз.

Система оценки

Есеп төрт бөлімнен тұрады:

$1 \le T \le 50, N = 2, 1 \le A_1 \le 10^6$. Бұл бөлім $10$ ұпайға бағаланады.
$1 \le T \le 50, N = 3, 1 \le A_1 \le 10^9 $. Бұл бөлім $15$ ұпайға бағаланады..
$T = 1, 1 \le N \le 50, 1 \le A_1 \le 10^5$. Бұл бөлім $30$ ұпайға бағаланады.
$1 \le T \le 1000, 1 \le N \le 50, 1 \le A_1 \le 10^{16}$. Бұл бөлім $45$ ұпайға бағаланады.

Пример:

Вход

2
3 13
2 10

Ответ

13 7 4 
10 6

Замечание

Бірінші тест: Басында 13, 7, 4. 1-шіден кейін : 2, 14, 8. 2-шіден кейін : 4, 4, 16. 3-шіден кейін: 8,8,8. ( Temirlan Satylkhanov )
комментарий/решение олимпиада

Есеп №6. (Аударулар)

Ограничение по времени:

1 second

Ограничение по памяти:

64 megabytes

Үстелдің үстінде $K$ қағаз жатыр. Сізге $N$ саны берілген. Әр қағазда 1 ден $N$-ге дейінгі әр сан бір реттен жазылған. Бірақ сандардың кейбірі қағаздың көрінетін бетінде ал қалғаны артқы бетінде жазылған. Сіздің тапсырмаңыз - осы қағаздардың кейбірін аудару, сол аударулардан кейін қағаздың көрінетін жақтарындағы әр түрлі сандардың санын көп қылу.

Формат входного файла

Бірінші қатарда $N$ және $K$ сандары берілген($N \times K\le 10^6$, $ N \ge 1 $ және $K \ge 1$). Келесі $K$ қатарда қағаздардың сипаттамалары берілген. $i+1$-ші қатарда $i$-ші кағаздың көрінетін бетіндегі сандар саны $m$($0 \le m \le N$) жазылған. Одан кейін $m$ сан $i$-ші қағаздың көрінетін бетіндегі сандар, әр сан $1$-ден $N$-ге дейін.

Формат выходного файла

$K$ символдан туратын қатар шығарыңыз. $i(1 \le i \le K)$ символ 1-ге тең егерде аудару керек болса, олай болмаса 0. Егер бірнеше жауап болса кез келгенін шығарыңыз.

Система оценки

Есеп бес бөлімнен тұрады:

$1 \leq N \leq 10$, $1 \le K \le 10$. Бұл бөлім $11$ ұпайға бағаланады.
$1 \leq N \le K$. Бұл бөлім $8$ ұпайға бағаланады.
$1 \leq N \leq 100$. Бұл бөлім $15$ ұпайға бағаланады.
$1 \leq N \times K \leq 5 \cdot 10^4$. Бұл бөлім $30$ ұпайға бағаланады.
$1 \leq N \times K \leq 10^6 $. Бұл бөлім $36$ ұпайға бағаланады.

Пример:

s Вход

Ответ

Вход

6 2
3 1 3 4
3 1 2 4

Ответ

( Temirlan Satylkhanov )
комментарий/решение олимпиада

Есеп №7. (Құпиялы алгоритмдер)

Ограничение по времени:

2 seconds

Ограничение по памяти:

256 megabytes

Timart елінде $N$ қала және $M$ екіжақты жол бар. Қалалар $1$-ден $N$-ге дейінгі сандармен белгіленген. Осы жолдар арқылы әр қаладан кез келген қалаға баруға болады. Андрей құпиялы алгоритмдер жазылған бүктеме қағаздарды Timart елінің қалаларында жасырып қойды. $i$-ші қалада $A_i$ бүктеме қағаз жасырылған. Рамазан осы бүктеме қағаздарды ұрлап кеткісі келеді. Рамазан өзі тұрған қаладағы барлық бүктеме қағаздарды ұрлап кете алады. Ол кез келген қаладан бастап ұрлай алады. Рамазан Андрейге ұсталып қалмас үшін, бір жолмен қатарынан екі рет жүрмейді. Әр қаладағы бүктеме қағаздарды бір рет ғана ұрлап кетуге болады, бірақ бір қалаға бірнеше рет баруға болады. Рамазан ең көп дегенде неше бүктеме қағаз ұрлай алады?

Формат входного файла

Бірінші жолда екі бүтін сан берілген $N$, $M$ ($1 \le N \le 5 \cdot 10^5$, $0 \le M \le 5 \cdot 10^5$). Екінші жолда $N$ бүтін сан жазылған $A_1, A_2, \ldots, A_N$, мұндағы $A_i$ ~— $i$-ші қаладағы бүктеме қағаздардың саны. Келесі $M$ жолда $2$ бүтін саннан жазылған $u_i$, $v_i$ ($1 \le u_i, v_i \le N, u_i \neq v_i$)~— $u_i$ және $v_i$ қалаларын қосатын жол бар. Екі әр түрлі қаланы байланыстыратын ең көп дегенде бір ғана жол болуы мүмкін. Осы жолдар арқылы әр қаладан кез келген қалаға жетуге болады.

Формат выходного файла

Бір бүтін сан шығарыңыз - берілген есептің жауабын.

Система оценки

Есеп бес бөлімнен тұрады:

$1 \le N \le 100$,$M = \frac{N \cdot (N - 1)}{2}$, $1 \le A_i \le 300$, барлық $1 \le i \le N$ үшін. Бұл бөлім $7$ ұпайға бағаланады.
$1 \le N \le 12$, $0 \le M \le 66$, $1 \le A_i \le 300$, барлық $1 \le i \le N$ үшін. Бұл бөлім $12$ ұпайға бағаланады.
$1 \le N \le 10^5$, $M = N - 1$, $1 \le A_i \le 10^9$, барлық $1 \le i \le N$ үшін. Бұл бөлім $12$ ұпайға бағаланады.
$3 \le N \le 10^5$, $M = N$, $1 \le A_i \le 10^9$, барлық $1 \le i \le N$ үшін. Бұл бөлім $25$ ұпайға бағаланады.
$1 \le N \le 5 \cdot 10^5$, $0 \le M \le 5 \cdot 10^5$, $1 \le A_i \le 10^9$, барлық $1 \le i \le N$ үшін. Бұл бөлім $44$ ұпайға бағаланады.

\Example Вход

8 8
1 2 3 4 5 6 7 8
1 2
2 3
2 4
2 5
5 6
6 7
7 8
8 5

Ответ

( Temirlan Satylkhanov )
комментарий/решение олимпиада

Есеп №8. (Тима және дәрежелер қосындысы)

Ограничение по времени:

1 second

Ограничение по памяти:

256 megabytes

Тимада $N$ бүтін саны және $N$ саннан тұратын $A$ массивы бар. Тағыда ода $M$ және $K$ бүтін сандары бар. Барлық $1$—ден $N$-$M$+$1$—ге дейінгі $i$ бүтін саны үшін Тима мынадай өрнектің $1^K \cdot A_{i} + 2^K \cdot A_{i + 1} + \cdots + M^K \cdot A_{i + M - 1}$ мәнің санағысы келеді. Оған осы есепті шығаруға көмектесіңіз.

Формат входного файла

Бірінші жолда үш бүтін сан берілген $N$($1 \le N \le 10^5$),$M$($1 \le M \le N$) және $K$($0 \le K \le 20$). Екінші жолда $N$ бүтін сан берілген $A_1,A_2, \cdots, A_N$ ($1 \le A_i \le 10^9$).

Формат выходного файла

$N$-$M$+$1$ жол шығарыңыз, $i$-ші жолда $1^K \cdot A_{i} + 2^K \cdot A_{i + 1} + \cdots + M^K \cdot A_{i + M - 1}$ өрнегінің мәнің $10^9 + 7$ бөлгендегі қалдығын шығарыңыз.

Система оценки

Есеп бес бөлімнен тұрады:

$1 \le N \le 100, 0 \le K \le 3,1 \le A_i \le 10$. Бөлім $7$ ұпайға бағаланады.
$1 \le N \le 10^4, 0 \le K \le 20,1 \le A_i \le 10^9$. Бөлім $12$ ұпайға бағаланады..
$1 \le N \le 10^5, 0 \le K \le 1,1 \le A_i \le 10^9$. Бөлім $13$ ұпайға бағаланады.
$1 \le N \le 10^5, K = 2,1 \le A_i \le 10^9$. Бөлім $20$ ұпайға бағаланады.
$1 \le N \le 10^5, 0 \le K \le 20,1 \le A_i \le 10^9$. Бөлім $48$ ұпайға бағаланады.

Примеры:

Вход

5 3 2
1 2 3 4 5

Ответ

36
50
64

Вход

3 2 0
7 3 2

Ответ

10
5

Замечание

Бірінші мысалға түсіндірме: $i = 1$ болғанда, $1^K \cdot A_1 + 2^K \cdot A_2 + 3^K \cdot A_3$ = $1^2 \cdot 1 + 2^2 \cdot 2 + 3^2 \cdot 3 = 1 + 8 + 27 = 36$. $i = 2$ болғанда, $1^K \cdot A_2 + 2^K \cdot A_3 + 3^K \cdot A_4$ = $1^2 \cdot 2 + 2^2 \cdot 3 + 3^2 \cdot 4 = 50$. $i = 3$ болғанда, $1^K \cdot A_3 + 2^K \cdot A_4 + 3^K \cdot A_5$ = $1^2 \cdot 3 + 2^2 \cdot 4 + 3^2 \cdot 5 = 64$. ( Temirlan Satylkhanov )
комментарий/решение олимпиада

Есеп №9.

Есеп F. Оңдаңыз!

Ограничение по времени:

1 second

Ограничение по памяти:

256 megabytes

Барлық сандары теріс емес массивты, Тима жақсы деп есептейді. Тиманың ұзындығы $n$ болатын, бүтін сандардан тұратын $a$ массивы бар. Тима оны жақсы еткісі келеді, сол үшін ол осындай операция істей алады:

$1 <= i,j <= n, i \ne j, 1 <= x <= 10^9$ және $a_i \ge x$ орындалатын $i,j, x$ сандарын таңдап алып, $a_i$ санынан $x$ санын азайтып, ал $a_j$ санына $x$ қосу. Осы операцияның құны $|i - j| \cdot x$ теңге.

Қалайда аз теңге қолданып, Тиманың массивын жақсы етіңіз.

Формат входного файла

Бірінші жолда екі бүтін сан $n, type (1 <= n <= 3 \cdot 10^5, 0 <= type <= 1)$ енгізіледі. Екінші жолда $n$ бүтін сан $a_1,a_2, ..., a_n(-10^8 <= a_i <= 10^8)$ енгізіледі. $a$ массивын жақсы ете алынуына кепілдік беріледі.

Формат выходного файла

Бірінші жолда массивты жақсы етуге құртылған тенге санын шығарыңыз. Егер $type = 1$ болса, екінші жолда бір бүтін сан $k (0 <= k <= 2 \cdot n)$ — операциялар санын шығарыңыз. Келесі $k$ жолда үш саннан $i,j,x(1 <= i,j <= n, i \ne j, 1 <= x <= 10^9)$ — операциялар сипаттамасын шығарыңыз. Операциялар санын азайтудың қажеті жоқ, бастысы құртылған тенге санын азайтыңыз. Егер $type = 0$ болса, басқа ештеңе шығарудың керегі жоқ.

Система оценки

Есеп сегіз бөлімнен тұрады:

Мысалдағы тесттер. 0 ұпайға бағаланады.
$n <= 10, type = 0, -1 <= a_i <= 1$. 8 ұпайға есептеледі.
$n <= 200, type = 0, -10 <= a_i <= 10, |a_1| + |a_2| + ... + |a_n| <= 400$. 16 ұпайға есептеледі.
$n <= 10^5, type = 0, -10^8 <= a_i <= 10^8, a_1 + a_2 + ... + a_n = 0$. 12 ұпайға есептеледі.
$n <= 2000, type = 0, -1 <= a_i <= 1$. 15 ұпайға есептеледі.
$n <= 3 \cdot 10^5, type = 0, -10^8 <= a_i <= 10^8, a_1 + a_2 + ... + a_n = 1$. 13 ұпайға есептеледі.
$n <= 3 \cdot 10^5, type = 0, -10^8 <= a_i <= 10^8$. 15 ұпайға есептеледі.
$n <= 3 \cdot 10^5, type = 1, -10^8 <= a_i <= 10^8$. 21 ұпайға есептеледі.

Примеры:

Вход

7 0
1 1 -1 0 -1 1 1

Ответ

Вход

4 1
4 -2 -2 1

Ответ

( Temirlan Satylkhanov )
комментарий/решение олимпиада

Есеп №10.

Есеп F. Оңдаңыз!

Ограничение по времени:

1 second

Ограничение по памяти:

256 megabytes

$1 <= i,j <= n, i \ne j, 1 <= x <= 10^9$ және $a_i \ge x$ орындалатын $i,j, x$ сандарын таңдап алып, $a_i$ санынан $x$ санын азайтып, ал $a_j$ санына $x$ қосу. Осы операцияның құны $|i - j| \cdot x$ теңге.

Қалайда аз теңге қолданып, Тиманың массивын жақсы етіңіз.

Формат входного файла

Формат выходного файла

Система оценки

Есеп сегіз бөлімнен тұрады:

Мысалдағы тесттер. 0 ұпайға бағаланады.
$n <= 10, type = 0, -1 <= a_i <= 1$. 8 ұпайға есептеледі.
$n <= 200, type = 0, -10 <= a_i <= 10, |a_1| + |a_2| + ... + |a_n| <= 400$. 16 ұпайға есептеледі.
$n <= 10^5, type = 0, -10^8 <= a_i <= 10^8, a_1 + a_2 + ... + a_n = 0$. 12 ұпайға есептеледі.
$n <= 2000, type = 0, -1 <= a_i <= 1$. 15 ұпайға есептеледі.
$n <= 3 \cdot 10^5, type = 0, -10^8 <= a_i <= 10^8, a_1 + a_2 + ... + a_n = 1$. 13 ұпайға есептеледі.
$n <= 3 \cdot 10^5, type = 0, -10^8 <= a_i <= 10^8$. 15 ұпайға есептеледі.
$n <= 3 \cdot 10^5, type = 1, -10^8 <= a_i <= 10^8$. 21 ұпайға есептеледі.

Примеры:

Вход

7 0
1 1 -1 0 -1 1 1

Ответ

Вход

4 1
4 -2 -2 1

Ответ

( Temirlan Satylkhanov )
комментарий/решение олимпиада

Есеп №11.

Есеп G. Қағаз, қайшы, тас

Уақытка қойылған шектеу:

1 second

Жадқа қойылған шектеу:

256 megabytes

$N + 1$ робот қағаз-қайшы-тас ойынынан турнирге қатысады, сол роботтың біреуі сіздікі. Осы турнирде әр робот өз программасын қолданады, програма келесі жүрістерден тұрады: 'R'(тас), 'P'(қағаз) және 'S'(қайшы). Қағаз тасты женеді, тас қайшыны женеді, қайшы қағазды женеді. Екі робот ойнаған кезде, кім бірінше жеңісті жүріс жасайды, сол ұтады. Басында екі робот өздерінің программаларының бірінші жүрісін жасайды. Егер екеуінің жасаған жүрістері әр түрлі болса, ойынның шарты бойынша жеңіс жүрісін жасаған ұтады. Егер жүрістері бірдей болса, әр робот өздерінің программалары бойынша келесі жүрістерін жасайды. Робот өзінің программасының соңғы жүрісін жасап және оған келесі жүріс жасау керек болса, ол өз программасының бірінші жүрісін жасайды. Егер ойын шексіз ұзақ болса, тең ойын болып саналады. Сіз кездейсоқ өзіңіздің $N$ қарсыластарыңыздың программаларын біліп қойдыңыз. Кез келген қарсыласты ұтатын, өз роботыңызға программа жазыңыз.

Оқу форматы

Бірінші жолда бір бүтін сан $N(1 <= N <= 100)$ берілген — қарсыластарыңыздың саны. Келесі $N$ жолда $C_i(1 <= |C_i| <= 100)$ — қарсыластарыңыздың программалары. $C_i$ ол 'R', 'P', 'S' символдарынан тұрады.

Жазу форматы

Егер жеңісті программа жазу мүмкін болмаса, "IMPOSSIBLE" деп шығарыңыз. Олай болмаса, жеңісті программаны шығарыңыз. Программаның ұзындығы $10^4$ тен аспау керек. Егер программа жазу мүмкін болса, онда ұзындыңы $10^4$тен аспайтын жеңісті программа жазуға болатының дәлелдеуге болады. Егер бірнеше дұрыс жауап болса, кез келгенің шығарыңыз.

Мысалдар:

Вход

3
R
S
P

Ответ

IMPOSSIBLE

Оқу

1
RP

Жауап

Оқу

2
RP
S

Жауап

RPP

( Temirlan Satylkhanov )
комментарий/решение(2) олимпиада

Есеп №12.

Есеп G. Қағаз, қайшы, тас

Уақытка қойылған шектеу:

1 second

Жадқа қойылған шектеу:

256 megabytes

Оқу форматы

Жазу форматы

Мысалдар:

Вход

3
R
S
P

Ответ

IMPOSSIBLE

Оқу

1
RP

Жауап

Оқу

2
RP
S

Жауап

RPP

( Temirlan Satylkhanov )
комментарий/решение(2) олимпиада

Есеп №13.

Есеп F. UCL Fantasy

Уақытка қойылған шектеу:

1 second

Жадқа қойылған шектеу:

256 megabytes

Жақында Данияр футболмен қызыға бастады. Бірден UCL Fantasy ойнап бастады . Әр адамда 15 ойыншы(2 қақпашы, 5 қорғаушы, 5 жартылай қорғаушы, 3 шабуылшы) УЕФА Чемпиондар лигасында ойнайтын. Әр ойыншы турда өз ойнағанына байланысты ұпай алып келеді. Ұпайды гол салған үшін, гол әкеп соққан пас, қақпашыға гол жібермеген үшін, қызыл карточка үшін теріс ұпай и т.д. Әр тур алдында Данияр состав таңдайды, составта 11 ойыншы және олардың арасында бір капитан болады. Составта бір қақпашы, және келесі схемалар бойынша ойнауға болады: 5(қорғаушы)-4(жартылай қорғаушы)-1(шабуылшы), 5-3-2,5-2-3,4-5-1,4-4-2,4-3-3,3-5-2,3-4-3. Даниярдың ұпайы, ол оның составындағы(11 ойыншы) ойыншылардың ұпайының қосындысы + капитанның ұпайы(сонда капитанның баллы екі еселенеді). Данияр өз ойыншыларының ұпайын біледі, оған турға ұпайы ең көп болатын состав таңдауға көмектесіңіз.

Оқу форматы

15 жолда ойыншылар туралы информация беріледі: $name_i(1 <= |name_i| <= 20)$,$position_i$ және $p_i(-10 <= p_i <= 100)$ — ойыншының аты, позициясы және турдағы ұпайы. Ішінде 2 қақпашы, 5 қорғаушы, 5 жартылай қорғаушы, 3 шабуылшы. $position_i$ осылардың біреуі : GK — қақпашы, DF — қорғаушы, MF — жартылай қорғаушы, FW — шабуылшы.

Жазу форматы

Даниярдың осы турда алатын ұпайын шығарыңыз.

Пример:

Оқу

Messi FW 10
Pique DF 6
Tadic FW 2
Coutinho MF 3
Stegen GK 7
Salah MF 2
Ziyech MF 6
Onana GK 6
Beek MF 8
Son MF 0
Alba DF 8
Suarez FW 8
Blind DF 6
Ligt DF 6
Roberto DF 6

Жауап

Түсініктеме

Messi капитан, ал состав мынадай болады:

( Temirlan Satylkhanov )
комментарий/решение(3) олимпиада

Есеп №14.

Есеп F. UCL Fantasy

Уақытка қойылған шектеу:

1 second

Жадқа қойылған шектеу:

256 megabytes

Оқу форматы

Жазу форматы

Даниярдың осы турда алатын ұпайын шығарыңыз.

Пример:

Оқу

Messi FW 10
Pique DF 6
Tadic FW 2
Coutinho MF 3
Stegen GK 7
Salah MF 2
Ziyech MF 6
Onana GK 6
Beek MF 8
Son MF 0
Alba DF 8
Suarez FW 8
Blind DF 6
Ligt DF 6
Roberto DF 6

Жауап

Түсініктеме

Messi капитан, ал состав мынадай болады:

( Temirlan Satylkhanov )
комментарий/решение(3) олимпиада

Есеп №15.

Задача F. K-sort

Ограничение по времени:

1 second

Ограничение по памяти:

256 megabytes

Есмаханда $N$ саннан тұратын $A$ массиві берілген $A_0,A_1,..,A_{N-1}$. Массив $k$-сортталатын деп аталады, егер келесі операцияны бірнеше(мүмкін 0) рет жасап, массивты кемімейтін қылдырып жасауға болса: $i(0 <= i < N)$ индексін таңдап, массивтегі $i$-ші және $((i + k)$ mod $N$)-ші элементтердің орның ауыстыру. Мұндағы $a$ mod $b$ дегеніміз $a$-ның $b$-ға бөлгендегі қалдығы. Мысалы, $7$ mod $3$ = 1, $8$ mod $4$ = 0, $5$ mod $11$ = 5. Массив кемімейтін деп саналады, егер бірінші элементтен басқа барлық элемент алдыңдағы элементтен кіші болмаса. Сізге $Q$ сұрау беріледі, әр сұрауда бір бүтін $k$ саны беріледі. Әр сұрау үшін $A$ массивы $k$-сортталатынба екенің аңықтау қажет.

Формат входного файла

Бірінші жолда екі бүтін сан $N,Q(1 <= N,Q <= 300000)$. Екінші жолда $N$ бүтін сан $A_0,A_1, ..., A_{N - 1}(1 <= A_i <= 10^9)$. Келесі $q$ жолда бір бүтін саннан $k_i(1 <= k_i <= N)$.

Формат выходного файла

$q$ жолда бір саннан шығарыңыз — $i$-ші жолда $1$ шығарыңыз, егер $A$ массивы $k_i$-сортталатын болса, болмаса 0 шығарыңыз.

Система оценки

Есеп 25 тесстен тұрады, әр тест 4 ұпайға бағаланады:

$1 <= N,Q <= 100$. Тест 1 -- 4
$1 <= N <= 100000, Q = 1$, $k_1 = N$. Тест 5 -- 7
$1 <= N,Q <= 2000$. Тест 8 -- 11
$1 <= N,Q <= 50000$. Тест 12 -- 15
$1 <= N,Q <= 300000$. Тест 16 -- 25

Пример:

Вход

Ответ

Замечание

$A={3,2,2,4}$, басқаша айтқанда $A_0 = 3, A_1 = 2, A_2 = 2, A_3 = 4$. Массив $3$-сортталатын, себебі келесі операциялармен сорттауға болады:

$i = 1$ таңдаймыз, сонда $(i + 3)$ mod $N = (1 + 3)$ mod $4 = 0$. Онда біз $A_1$ және $A_0$ орның ауыстырамыз. Содан кейін $A = {2,3,2,4}$ болады.
$i = 2$ таңдаймыз, сонда $(i + 3)$ mod $N = (2 + 3)$ mod $4 = 1$. Онда біз $A_2$ және $A_1$ орның ауыстырамыз. Содан кейін $A = {2,2,3,4}$ болады.

( Temirlan Satylkhanov )
комментарий/решение(1) олимпиада

Есеп №16.

Есеп B. Тетрис

Ограничение по времени:

1 second

Ограничение по памяти:

256 megabytes

BThero тетрис ойнап отыр. Тетрис алаңың ұзындығы $W$ және биіктігі шексіз болатын тіктөртбұрыш ретінде қарастыруға болады. Ыңғайлы болу үшін алаңды жазықтықта орналастырайық. Алаңның төмендегі сол жақтағы ұяшығы $(1, 1)$ координатында, ал төмендегі оң жақтағы ұяшығы $(W, 1)$ координатасында орналасқан. Ойында кезекпен $q$ екі түрлі оқиға болды:

Алаңға $x$-координат бойынша $[l,r]$ кесіндісінде биіктігі $h$ болатын жаңа тіктөртбұрыш құлайды. Ол шексіз биіктіктен бастап басқа тіктөртбұрышқа тірелгенше немесе алаңның түбіне жеткенде дейін құлайды. Бұл тетрис ойынында тіктөртбұрыштарды қозғалтуға болмайды.
$y$ деген бүтін санмен бірге сұратым келеді. Осы $y$ биіктігінде қанша ұяшық тіктөртбұрыштардың ішінде екенін жауап беру керек.

BThero ағамызға бүкіл сұратымдарға жауап беруге көмектесіңіз!

Формат входного файла

Кіріс деректердің бірінші жолында $W$ және $q$ бүтін сандары берілген ($1 <= W <= 10^6$, $2 <= q <= 10^5$). Келесі $q$ жолдарда оқиғалардың сипаттамалары берілген. Алдымен бір бүтін сан $t$ — оқиғаның түрі беріледі. Егер $t = 1$ болса, бұл бірінші түрдегі оқиға және сізге қосымша үш бүтін сан $l$, $r$ және $h$ беріледі ($1 <= l <= r <= W$, $1 <= h <= 10^6$). Егер $t = 2$ болса, бұл екінші түрдегі оқиға және сізге қосымша бір бүтін сан $y$ беріледі ($1 <= y <= 10^9$). Оқиғалар арасында кем дегенде бір бірінші түрдегі оқиға және кем дегенде бір екінші түрдегі оқиға бар.

Формат выходного файла

Шығыс деректерде бүкіл сұратымдардың жауаптары болу керек.

Система оценки

Есеп $6$ бөлімнен тұрады:

$q <= 5000$. $20$ ұпайға бағаланады.
Ең бірінші оқиға бірінші түрдегі оқиға, ал бүкіл қалған оқиғалар екінші түрдегі оқиғалар. $10$ ұпайға бағаланады.
Бүкіл тіктөртбұрыштардың ұзындығы $1$, ені $1$ және бүкіл сұратымдарда $y <= 10^6$. $10$ ұпайға бағаланады.
Бүкіл тіктөртбұрыштардың ұзындығы $1$ және бүкіл сұратымдарда $y <= 10^6$. $20$ ұпайға бағаланады.
Бүкіл сұратымдарда $y <= 10^6$. $20$ ұпайға бағаланады.
Есептің толық шарттары. $20$ ұпайға бағаланады.

Пример:

Вход

Ответ

Замечание

( Temirlan Satylkhanov )
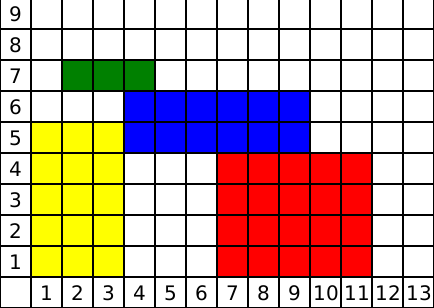
комментарий/решение олимпиада

Есеп №17.

Есеп C. Футболкалар

Ограничение по времени:

1 second

Ограничение по памяти:

256 megabytes

Тима футболкаларды жақсы көреді. Қалада $1$-ден $n$-ға дейін нөмірленген $n$ түсті футболкалар сататын өте керемет футболкалар дүкені бар. $k$ күн ішінде дүкен ауқымды акция өткізеді, онда олар кейбір түстердің футболкаларын жарты бағамен сатады. Дүкен өзінің веб-сайтында $a$ кестесін жариялады. Мұнда $a_{i,j}$ акция $j$-ші күні $i$-ші түсті футболкаға жарамдылығын көрсетеді (егер жарамды болса 1, әйтпесе 0). Тимада $1$-ден $n$-ға дейінгі сандарды алмаластыруы болып табылатын $p$ түстерін таңдау тәртібі бар. Тиманың сүйікті түсі - $p_1$ түсі, екінші сүйіктісі - $p_2$ түсі және т.б. Күн сайын $k$ күн ішінде ол дүкенге келіп, және сол күні акция жарамды түстердің ішінде ол ең сүйікті түсі бар бір футболка сатып алады. Басқаша айтқанда, $i $ күні ол $a_{i,{p_j}} = 1$ болатын ең төменгі $j$ таңдайды және $p_j$ түсі бар бір футболка сатып алады. Егер сол күні акцияның бір түсі болмаса, онда ол ештеңе сатып алмайды. Тима $p$ алмастыруын құпияда сақтайды. Ол $k$ күнде сатып алған футболкалар арасында әртүрлі түстердің максималды саны қандай болуы мүмкін?

Формат входного файла

Бірінші жолда екі бүтін сан берілген $n$ және $k$ ($1 <= n <= 10^5$, $1 <= k <= 14$). Келесі $n$ жолдарда $k$ таңбадан — $a$ элементтері берілген. Әр таңба «0» немесе «1».

Формат выходного файла

Бір бүтін санды — футболкалар арасында болуы мүмкін түрлі түстердің максималды саны шығарыңыз.

Система оценки

Есеп $6$ бөлімнен тұрады:

Есептің шартында берілген тесттер. $0$ ұпайға бағаланады.
$n$, $k <= 2$. $9$ ұпайға бағаланады.
$n$, $k <= 8$. $18$ ұпайға бағаланады.
$n$, $k <= 14$. $22$ ұпайға бағаланады.
$n <= 10000$, $k <= 14$. $29$ ұпайға бағаланады.
Есептің толық нұсқасы. $22$ ұпайға бағаланады.

Примеры:

Вход

Ответ

Вход

Ответ

( Temirlan Satylkhanov )
комментарий/решение олимпиада

Есеп №18.

Есеп A. Спорттық бағдарламаушылар

Ограничение по времени:

1 second

Ограничение по памяти:

256 megabytes

Қазақстанның спорттық бағдарламаушылар ассоциациясы жүгіруден жарыс өткізді. Жарысқа $N$ жүгіруші қатысты. Басында жүгірушілер $1$-ден $N$-ге дейін бірі артынан бірі орналасты. Жарыс басталғанда олар сол ретті бұзбай жүгіре бастады. Нөмірі $1$ болатын жүгіруші бірінші, ал нөмірі $N$ болатын жүгіруші — соңғы. Бірақ қандай жарыста ешкім ешкімді озбайды? Бір жүгірушінің бауы шешіліп кеткенде ғана олардың реті өзгере алады. Жүгіруші бауын байлап жатқанда одан кейін келе жатқан бірнеше адам оны озып кетуі мүмкін. Мысалы, $N = 5$ жүгіруші жарысқа қатысқан кезде бастапқы қатар осындай болады: $1$ $2$ $3$ $4$ $5$. Біраз уақыттан кейін $2$-ші жүгірушінің бауы шешіліп кетті дейік. Ол бауын байлап жатқан уақытта оны екі жүгіруші озып кетті дейік. Онда олардың ендігі реті осындай болады: $1$ $3$ $4$ $2$ $5$. Егер бұдан кейін $4$-ші жүгірушінің бауы шешілсе, және сол үшін оны бір адам озып кетсе, жаңа рет мынадай болады: $1$ $3$ $2$ $4$ $5$. Сізге $N$ және жүгірушілердің мәреге келген реті беріледі. Сізге ең кем дегенде неше жүгірушінің бауы шешіліп кеткенін айту керек.

Формат входного файла

Бірінші жолда бір бүтін сан $N(1 <= N <= 200000)$ — жүгірушілердің саны беріледі. Екінші жолда $N$ бүтін сан $p_1, p_2, \ldots, p_N$($1 <= p_i <= N$, $i \neq j$ болса $p_i \neq p_j$) беріледі. Мәреге бірінші болып $p_1$ келді, екінші болып $p_2$, \ldots, соңғы болып $p_N$ келді.

Формат выходного файла

Бір бүтін сан — есептің жауабын шығарыңыз.

Примеры:

Вход

6
1 2 5 4 3 6

Ответ

Вход

3
1 2 3

Ответ

Замечание

Бірінші мысалды қарастырайық. Басында қатар: $1$ $2$ $3$ $4$ $5$ $6$. Мүмкін жағдайлардың бірі: $4$-ші жүгірушінің бауы шешіліп кетті, байлап жатқанда $5$ оны озып кетті. Ендігі рет: $1$ $2$ $3$ $5$ $4$ $6$ болды. Одан кейін $3$-ші жүгірушінің бауы шешіліп кетті және оны $5$ пен $4$ озып кетті. Ендігі қатар $1$ $2$ $5$ $4$ $3$ $6$ болды. Екіден аз адамның бауы шешіліп кетсе, онда берілген қатарға қол жеткізу мүмкін емес болатынын көрсетуге болады. ( Temirlan Satylkhanov )
комментарий/решение(7) олимпиада

Есеп №19.

Есеп A. Жұмыс па әлде демалыс па?

Ограничение по времени:

1.5 seconds

Ограничение по памяти:

256 megabytes

Адиде $S$ теңге бар. Келесі $N$ күннің әрқайсысында ол немесе күні бойы жұмыс жасаймын, немесе күні бойы демаламын деп шешті. Егер $i$-ші күні жұмыс жасаса Ади $a_i$ теңге табады. Ал кесірінше, $i$-ші күні демаламын десе $b_i$ теңге кетіреді. Басқаша айтқанда, егер $i$-ші күні жұмыс жасаса, онда оның ақшасы $a_i$ тенгеге көбейеді, ал демалса, $b_i$-ға азаяды. Ең көп дегенде Ади неше күн демала алады? Ешқандай уақытта оның ақшасы теріс сан болып кетпеу керек.

Формат входного файла

Бірінші жолда $N$ және $S$($1 <= N <= 200000$, $0 <= S <= 10^9$) — күндер саны және бастапқыдаға ақша саны бар. Келесі $N$ жолда екі бүтін сан $a_i$ және $b_i(0 <= a_i,b_i <= 10^9)$ беріледі.

Формат выходного файла

Жалғыз бүтін сан — есептің жауабың шығарыңыз.

Примеры:

Вход

Ответ

Вход

Ответ

Замечание

Бірінші мысалда: бірінші күні жұмыс жасайды, ал екінші және үшінші күні демалады. Екінші мысалда: ол $2$, $4$ және $5$ күндері демалады. ( Temirlan Satylkhanov )
комментарий/решение(2) олимпиада

Есеп №20.

Есеп С. Массивтөбедегі сайлау

Ограничение по времени:

2 seconds

Ограничение по памяти:

1024 megabytes

Массивтөбе қаласында әкім сайлауы болайын деп жатыр. Массивтөбеде $n$ үй және оларды байланыстыратын $n - 1$ жол бар. Осы жолдар арқылы әр үйден кез келген үйге жетуге болады. Айбар жаңа бастап жүрген блогер. Ол бір жай жолмен жүріп үйдің адамы кімге дауыс беретінің сұрауды видеоға түсіруді шешті. Жай жол деп, әр үйден жәңе әр жолдан ең көп дегенде бір рет өтетін жолды айтамыз. Айбар біледі, видеода көп қарау болмайды, егер ода доминант үміткер болмаса. Үміткер доминант деп аталады, егер ол сұралған адамдардың ішінде жартысынан көп дауыс алатын болса. Сізге $v_1, v_2, ..., v_n$ әр үйдің адамы кімге дауыс берілетіні айтылады. Қызық контент жасау үшін Айбар, доминанты бар қанша әр түрлі жол бар екенің санағысы келеді. $v$ үйінен $u$ға, $u$ үйінен $v$-ға жолдары бірдей болып саналады.

Формат входного файла

Бірінші жолда $n(1 <= n <= 77777)$. Екінші жолда $n$ бүтін сан $v_1,v_2,..,v_n(1 <= v_i <= n)$. Келесі $n - 1$ жолда екі бүтін сан $a$ және $b(1 <= a,b <= n)$ — $a$ және $b$ үйлерінің арасында жол бар екенің айтады.

Формат выходного файла

Есептің жауабын шығарыңыз.

Система оценки

Есеп $9$ бөліктен тұрады, әр бөлікте келесі шарттар орындалады:

Берілген мысалдар. $0$ ұпайға бағаланады.
$n <= 100$. $a_i=i$, $b_i=i+1$ барлық $i$ ($1 <= i < n$) үшін. $6$ ұпайға бағаланады.
$n <= 2000$. $a_i=i$, $b_i=i+1$ барлық $i$ ($1 <= i < n$) үшін. $7$ ұпайға бағаланады.
$n <= 2000$. $8$ ұпайға бағаланады.
$a_i=1$, $b_i=i+1$ барлық $i$ ($1 <= i < n$) үшін. $10$ ұпайға бағаланады.
$v_i <= 100$. $a_i=i$, $b_i=i+1$ барлық $i$ ($1 <= i < n$) үшін. $9$ ұпайға бағаланады.
$a_i=i$, $b_i=i+1$ барлық $i$ ($1 <= i < n$) үшін. $13$ ұпайға бағаланады.
$v_i <= 100$. $12$ ұпайға бағаланады.
Берілгеніндегі шарттар. $35$ ұпайға бағаланады.

Пример:

Вход

Ответ

( Temirlan Satylkhanov )
комментарий/решение олимпиада

Есеп №21.

Есеп В. AB

Ограничение по времени:

1 second

Ограничение по памяти:

256 megabytes

A,B сыныптарынан $N$ оқушы бір қатарда тұр. $i$-ші тұрған оқушы, оның сол жағында $c_i$ оқушы оның сыныбынан емес екенің айтты. Сізге $c$ массивіндегі сандарды араластырып береді. Кез келген оқушылардың орналасу тәртібің табыңыз.

Формат входного файла

Бірінші жолда бір бүтін сан $N(1 <= N <= 1.5\cdot 10^6)$. Екінші жолда $N$ бүтін сан $x_1,x_2,...,x_N(0 <= x_i <= N)$ — $c$ массивын араластырылуы.

Формат выходного файла

Оқушылардың бастапқы орналасу тәртібің $a$ жәңе $b$ символынын тұратын, ұзындығы $N$ болатын сөз ретінде шығарыңыз. Егер бірнеше мүмкін дұрыс жауап болса, кез келгенің шығарыңыз.

Система оценки

Есеп $9$ бөлімнен тұрады:

Берілгеніндегі мысал. $0$ ұпайға бағаланады.
$N <= 10^5$. B сыныбынан бірде бір оқушы болмайтындай жауабы бар. $6$ ұпайға бағаланады.
$N <= 20$. $10$ ұпайға бағаланады.
$N <= 10^5$. B сыныбынан 2 оқушыдан көп болмайтындай жауабы бар. $8$ ұпайға бағаланады.
$N <= 10^5$. $c$ массивы $x$ массивына орын араластырмай тең болатын оқушылардың орналасу тәртібі бар. $14$ ұпайға бағаланады.
$N <= 40$. $13$ ұпайға бағаланады.
$N <= 2000$. $10$ ұпайға бағаланады.
$N <= 300000$. $27$ ұпайға бағаланады.
$N <= 1500000$. $12$ ұпайға бағаланады.

Примеры:

Вход

4
1 0 2 0

Ответ

bbab

Вход

5
0 0 2 1 3

Ответ

bbaba

Замечание

Егер $bbab$ бастапқы орналасу тәртібі болса, онда $c_1 = 0, c_2 = 0, c_3 = 2, c_4 = 1$ болады. Араластыру арқылы [1,0,2,0] массивін алуға болады. ( Temirlan Satylkhanov )
комментарий/решение олимпиада

Есеп №22.

Есеп D. Витя - тасбақа-ниндзя 2

Ограничение по времени:

1 second

Ограничение по памяти:

256 megabytes

Әр торында бір сан жазылған $N \times M$ кестесі беріледі. Витя сол жақ жоғарғы торда орналасқан, оның мақсаты-төменгі оң жақ бұрышқа жету. Бір қадамда оған көрші торға оңға немесе төменге (солға және жоғарыға жылжуға тыйым салынады) өтуге рұқсат етіледі. Торда болғаны үшін Витя осы торда көрсетілген санды төлеуі керек. Дончик кестенің иесі. Ол өзінің досы Витяға жеңілдік жасауға шешім қабылдады - сол жақ жоғарғы бұрыштан төменгі оң жаққа дейінгі жолда ең қымбат(ең үлкен сан жазылған) $K$ торға ғана төлеуге рұқсат берді. Витя өз мақсатына жету үшін ең аз дегенде қанша ақша жұмсайды?

Формат входного файла

Бірінші жолда үш бүтін сан $N,M$ және $K$ ($1 <= N, M <= 500$, $1 <= K <= N + M - 1$) беріледі. Келесі $N$ жолда $M$ саннан беріледі — $i$-ші жолдағы $j$-ші сан $a_{i, j}$ ($0 <= a_{i, j} <= 500$) $i$-ші жолда және $j$-ші бағанда жазылған сан.

Формат выходного файла

Жалғыз бүтін сан — есеп жауабың шығарыңыз.

Примеры:

Вход

Ответ

Вход

Ответ

Замечание

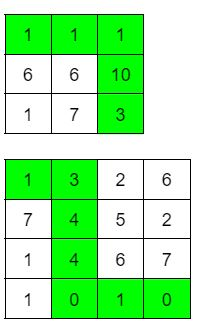
Жасыл түспен Витяның жүрген жолы белгіленген.

Бірінші мысалды ол барлық жүрген торлары үшін төлейді. Екінші мысалда, мәні $1,3,4,4,0,1,0$ деген торлар арқылы өтіп, ең қымбат екеуі($K = 2$) үшін $4 + 4 = 8$ төлеген ең қолайлы болады. ( Temirlan Satylkhanov )
комментарий/решение(1) олимпиада

Есеп №23.

Задача A. Үш қала

Ограничение по времени:

1 second

Ограничение по памяти:

256 megabytes

Бір кішкентай мемлекетте үш қала және солардың арасында үш ақылы жол бар. Бірінші жол $1$ мен $2$ші қаланы қосады, бұл жолмен өту $A$ теңге тұрады. Екінші жол $2$ мен $3$ші қаланы қосады, бұл жолмен өту $B$ теңге тұрады. Үшінші жол $1$ мен $3$ші қаланы қосады, бұл жолмен өту $C$ теңге тұрады. Парасатқа аз ақша кетіріп $1$ші қаладан $3$ші қалаға жету қажет.

Формат входного файла

Жалғыз жолда $A$, $B$, $C$($1 <= A,B,C <= 5000$) сандары беріледі.

Формат выходного файла

$1$ші қаладан $3$ші қалаға жетудің ең төмен құның шығарыңыз.

Система оценки

Бұл есеп $10$ тесттен тұрады, әр тест $10$ ұпайға бағаланады.

Примеры:

Вход

10 7 15

Ответ

Вход

200 300 700

Ответ

Замечание

Екінші мысалда: Парасатқа $2$ші қала арқылы барған тиімдірек. ( Temirlan Satylkhanov )
комментарий/решение(4) олимпиада

Есеп №24.

Есеп C. Тасымалсыз

Ограничение по времени:

1 second

Ограничение по памяти:

256 megabytes

Кішкентай Дамир сандарды қосқанда тасымал жасауды білмейді. Бірақ қосқанда тасымал жасау керек болмаса, ол дұрыс санайды. Мысалға, Дамир $27+5$-ті санай алмайды, бірақ $31421 + 6374 + 3$-ті оңай санай алады. Сізде $N$ сан бар. Олардың ішінен қосқанда тасымал жасамайтындай ең көп қанша сан таңдауға болады?

Формат входного файла

Бірінші жолда бір бүтін сан $N(1 <= N <= 18)$ беріледі. Екінші жолда $N$ бүтін сан $a_1, a_2, ..., a_N$($1 <= a_i <= 10^8$) беріледі.

Формат выходного файла

Есептің жауабын шығарыңыз.

Система оценки

Бұл есепте $10$ тест. Әр тест $10$ ұпайға бағаланады.

Тест 1. Берілген мысал.
Тест 2-4: $n = 2$.
Тест 5-7: $1 <= a_i <= 9$.
Тест 8-10: қосымша шектеу жоқ.

Пример:

Вход

5
8 45 32 27 111

Ответ

Замечание

Бірінші мысалда үш сан таңдауға болады: $45$,$32$,$111$. ( Temirlan Satylkhanov )
комментарий/решение(1) олимпиада

Есеп №25.

Есеп B. Балмұздақтың бағасы

Ограничение по времени:

1 second

Ограничение по памяти:

256 megabytes

Сіз балмұздақ сатасыз. Балмұздақтың өзіндік құны $k$ теңге. Ол дегеніміз, егер балмұздақты $x$ теңгеден сатсаныз, онда әр балмұздақтан табатын табысыңыз $x - k$ теңге болады. $n$ клиент бар. Әр клиент $i$ үшін оның балмұздаққа $s_i$ теңге құрта алатыны белгілі. Әр клиент қанша балмұздаққа ақшасы жетеді, соншама балмұздақ сатып алады. Өзіңіздің табысыңыз барынша көп болатындай балмұздақтын бағасын таңдаңыз.

Формат входного файла

Бірінші жолда екі бүтін $n,k$($1 <= n <= 2 \cdot 10^5$, $0 <= k <= 10^6$) — клиенттер саны және бір балмұздақтың өзіндің құны. Екінші жолда $n$ бүтін сан $s_1, s_2, \cdots, s_n$($1 <= s_i <= 10^6$) беріледі.

Формат выходного файла

Ең көп қанша пайда алатыңызды шығарыңыз.

Примеры:

Вход

5 2
8 9 10 15 12

Ответ

Вход

3 20
15 10 20

Ответ

Замечание

Бірінші мысалда балмұздақтың бағасын $7$ теңге қойған тиімдірек. Онда төртінші клиент 2 балмұздақ сатып алады, ал қалғандары бір бірден алады. Барлығы 6 балмұздақ сатылады. Әр балмұздақтан келетін табыс $5$($7 - 2$) теңге, онда барлығы $6 \cdot 5 = 30$ теңге пайда болады. ( Temirlan Satylkhanov )
комментарий/решение олимпиада

Есеп №26.

Есеп E. Графты бояу

Ограничение по времени:

1 second

Ограничение по памяти:

256 megabytes

$N$ төбеден және $M$ бағытталған қырдан тұратын тұзақсыз граф беріледі. Төбелер $1$ден $N$ге дейн сандармен нөмірленген. Графта $1$ мен $N$ төбесін қосатын қыр жоқ. Басында барлық төбе ақ түспен боялған. Мансұрға дәл $B$ төбені қара түске бояу қажет. Боялған соң, екі шетінің түсі бірдей болатын қырлар жойылып кетеді. Екі шетінің түсі бірдей қырлар жойылған соң, $1$-ден $N$-ге жол болмайтындай Мансұрға боялатын $B$ нүктеңі таңдауға көмектесіңіз .

Формат входного файла

Әр тестте бірнеше кіріс жиынтығы бар. Бірінші жолда бір бүтін сан $T$($1 <= T <= 100$) — кіріс деректер жиындарының саны. Әрбір кіріс деректер жиынтығының бірінші жолында үш бүтін сан $N$,$M$ және $B$($3 <= N <= 10^5$, $0 <= M <= min(2 \cdot 10^5,\frac{N \cdot (N - 1)}{2})$, $1 <= B <= N$) беріледі. Келесі $M$ жолда екі бүтін саннан $u$ және $v$($1 <= u, v <= N$, $u \ne v$, $(u,v) \ne (1, N)$) — $u$дан $v$ға бағытталған қыр. Графта қайталанатын қырлар жоқ және граф тұзақсыз. Тұзақсыз деген бір төбеден бастап, бірнеше қыр арқылы өтіп өзіне қайтып келуге болмайды дегенді білдіреді. Әр тесттегі $N$-дердің қосындысы $10^6$дан аспайды. Әр тесттегі $M$-дердің қосындысы $10^6$дан аспайды.

Формат выходного файла

Есеп шартына сәйкес бояуға болмаса <<-1>> шығарыңыз. Болса, $B$ бүтін сан — қараға бояу керек төбелердің нөмерлерін шығарыңыз. Егер бірнеше дұрыс жауап болса, кез келгенің шығаруға болады.

Пример:

Вход

Ответ

1 8 10 7 9
2 3

Замечание

( Temirlan Satylkhanov )
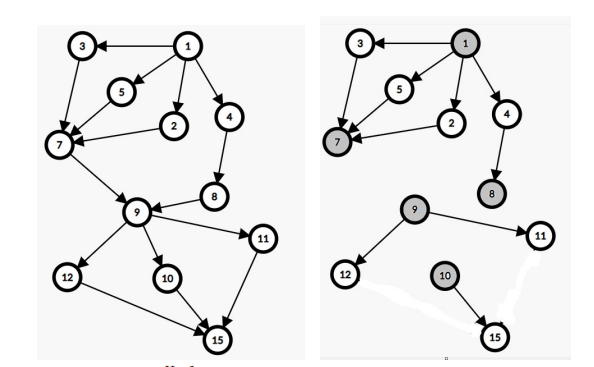
комментарий/решение олимпиада

Есеп №27.

Есеп F. XOR-сумма

Ограничение по времени:

2 seconds

Ограничение по памяти:

512 megabytes

$n$ бүтін оң саннан тұратын $a$ массиві берілген. $1$-ден $m$-ге дейінгі әрбір бүтін $k$ саны үшін $(a_1 \bmod k) \oplus (a_2 \bmod k) \oplus \ldots \oplus (a_n \bmod k)$ мәнін табыңыз. Бұл жерде $\oplus$ биттік XOR немесе болдырмау НЕМЕСЕ операциясын білдіреді. Бұл операция барлық заманауи бағдарламалау тілдерінде бар, С++, Python және Java тілінде <<^>>, ал Pascal тілінде <>. Бұл жерде $\bmod$ бөлгендегі қалдықты білдіреді. Яғни, $(a \bmod b)$ — $a$ санын $b$ санына бөлгендегі қалдық.

Формат входного файла

Бірінші жолда екі бүтін сан $n$ және $m$ ($1 <= n, m <= 500\,000$) беріледі. Екінші жолда $a_1, a_2, \ldots, a_n$ ($1 <= a_i <= m$) массиві беріледі.

Формат выходного файла

Бос орын арқылы $m$ бүтін сан шығарыңыз, ол жерде $k$-ші сан $(a_1 \bmod k) \oplus (a_2 \bmod k) \oplus \ldots \oplus (a_n \bmod k)$ мәніне тең болуы қажет.

Примеры:

Вход

4 5
2 5 4 2

Ответ

0 1 3 1 4

Вход

10 12
1 2 4 8 9 10 11 12 3 5

Ответ

0 1 1 1 0 1 0 5 9 3 11 1

( Temirlan Satylkhanov )
комментарий/решение олимпиада