4-й этап Республиканской олимпиады по информатике 2021-2022, 2 тура

Задача D. Витя - черепашка ниндзя 2

Ограничение по времени:

1 секунда

Ограничение по памяти:

256 мегабайт

Дается прямоугольная таблица $N \times M$, в каждой клетке записано какое-то число. Витя находится в левой верхней клетке, его цель добраться до правого нижнего угла. За один ход ему разрешается перемещаться в соседнюю клетку либо вправо, либо вниз (влево и вверх перемещаться запрещено). За посещение клетки, Витя должен платить число указанное в этой клетке. Дончик владелец таблицы. Он решил сделать скидку своему другу Вите, разрешив платить только за самые дорогие(наибольшие по значению) $K$ клеток на его пути от левого верхнего угла в правый нижний. Какое минимальное количество денег потратит Витя для достижения своей цели?

Формат входного файла

В первой строке даны три целых числа $N,M$ и $K$ ($1 <= N, M <= 500$, $1 <= K <= N + M - 1$). В следующих $N$ строках даны по $M$ целых чисел — $j$-е число на $i$-й строке $a_{i, j}$ ($0 <= a_{i, j} <= 500$) является числом на клетке в $i$-й строке и $j$-м столбце таблицы.

Формат выходного файла

Выведите одно целое число — ответ на задачу.

Примеры:

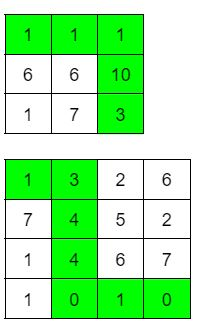
Вход

3 3 5
1 1 1
6 6 10
1 7 3

Ответ

16

Вход

4 4 2
1 3 2 6
7 4 5 2
1 4 6 7
1 0 1 0

Ответ

8

Замечание

Зеленым выделен путь Вити.

В первом примере, он заплатит за все посещенные клетки. Во втором примере, оптимально будет пройти через клетки со значениями $1,3,4,4,0,1,0$, и заплатит за максимальные два($K = 2$) из них, т.е $4 + 4 = 8$. ( Temirlan Satylkhanov )

Комментарий/решение

#include <iostream>

#include <vector>

#include <algorithm>

using namespace std;

const int MAXN = 1000;

int n, m, k;

int a[MAXN][MAXN];

int dp[MAXN][MAXN];

int main() {

cin >> n >> m >> k;

for (int i = 0; i < n; i++) {

for (int j = 0; j < m; j++) {

cin >> a[i][j];

}

}

dp[0][0] = a[0][0];

for (int i = 1; i < n; i++) {

dp[i][0] = max(dp[i-1][0], a[i][0]);

}

for (int j = 1; j < m; j++) {

dp[0][j] = max(dp[0][j-1], a[0][j]);

}

for (int i = 1; i < n; i++) {

for (int j = 1; j < m; j++) {

dp[i][j] = a[i][j] + max(dp[i-1][j], dp[i][j-1]);

}

}

cout << dp[n-1][m-1] - k << endl;

return 0;

}