4-й этап Республиканской олимпиады по информатике 2021-2022, 2 тура

Есеп D. Витя - тасбақа-ниндзя 2

Ограничение по времени:

1 second

Ограничение по памяти:

256 megabytes

Әр торында бір сан жазылған $N \times M$ кестесі беріледі. Витя сол жақ жоғарғы торда орналасқан, оның мақсаты-төменгі оң жақ бұрышқа жету. Бір қадамда оған көрші торға оңға немесе төменге (солға және жоғарыға жылжуға тыйым салынады) өтуге рұқсат етіледі. Торда болғаны үшін Витя осы торда көрсетілген санды төлеуі керек. Дончик кестенің иесі. Ол өзінің досы Витяға жеңілдік жасауға шешім қабылдады - сол жақ жоғарғы бұрыштан төменгі оң жаққа дейінгі жолда ең қымбат(ең үлкен сан жазылған) $K$ торға ғана төлеуге рұқсат берді. Витя өз мақсатына жету үшін ең аз дегенде қанша ақша жұмсайды?

Формат входного файла

Бірінші жолда үш бүтін сан $N,M$ және $K$ ($1 <= N, M <= 500$, $1 <= K <= N + M - 1$) беріледі. Келесі $N$ жолда $M$ саннан беріледі — $i$-ші жолдағы $j$-ші сан $a_{i, j}$ ($0 <= a_{i, j} <= 500$) $i$-ші жолда және $j$-ші бағанда жазылған сан.

Формат выходного файла

Жалғыз бүтін сан — есеп жауабың шығарыңыз.

Примеры:

Вход

3 3 5
1 1 1
6 6 10
1 7 3

Ответ

16

Вход

4 4 2
1 3 2 6
7 4 5 2
1 4 6 7
1 0 1 0

Ответ

8

Замечание

Жасыл түспен Витяның жүрген жолы белгіленген.

Бірінші мысалды ол барлық жүрген торлары үшін төлейді. Екінші мысалда, мәні $1,3,4,4,0,1,0$ деген торлар арқылы өтіп, ең қымбат екеуі($K = 2$) үшін $4 + 4 = 8$ төлеген ең қолайлы болады. ( Temirlan Satylkhanov )

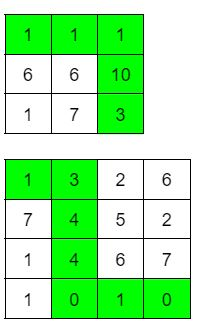
Комментарий/решение

#include <iostream>

#include <vector>

#include <algorithm>

using namespace std;

const int MAXN = 1000;

int n, m, k;

int a[MAXN][MAXN];

int dp[MAXN][MAXN];

int main() {

cin >> n >> m >> k;

for (int i = 0; i < n; i++) {

for (int j = 0; j < m; j++) {

cin >> a[i][j];

}

}

dp[0][0] = a[0][0];

for (int i = 1; i < n; i++) {

dp[i][0] = max(dp[i-1][0], a[i][0]);

}

for (int j = 1; j < m; j++) {

dp[0][j] = max(dp[0][j-1], a[0][j]);

}

for (int i = 1; i < n; i++) {

for (int j = 1; j < m; j++) {

dp[i][j] = a[i][j] + max(dp[i-1][j], dp[i][j-1]);

}

}

cout << dp[n-1][m-1] - k << endl;

return 0;

}