4-й этап Республиканской олимпиады по информатике 2021-2022, 2 тура
Задача A. Покраска суммой
Ограничение по времени:
1 секунда
Ограничение по памяти:
256 мегабайт
У вас есть массив целых чисел $a_1, \ldots, a_n$ размера $n$. Изначально каждое число массива покрашено в белый цвет. За одну операцию вы можете:
- Выбрать три белых числа $(a_i, a_j, a_k)$ ($1 <= i, j, k <= n$, $i \neq j$, $i \neq k$, $j \neq k$).
- Если значение $a_i + a_j$ строго больше $a_k$, покрасить $a_k$ в черный цвет.
Формат входного файла
В первой строке входного файла дано одно целое число $n$ — размер массива ($3 <= n <= 10^5$).
Во второй строке даны $n$ целых чисел $a_1, \ldots, a_n$ ($-10^9 <= a_i <= 10^9$).
Формат выходного файла
Выведите одно целое число — количество всевозможных конечных раскрасок. Можно показать, что в заданных ограничениях ответ никогда не превосходит $10^{18}$.
Примеры:
Вход 3 2 2 5Ответ
2Вход
4 -3 1 2 2Ответ
3
комментарий/решение(2) Проверить мое решение
Задача B. MEXI
Ограничение по времени:
1.5 секунд
Ограничение по памяти:
512 мегабайт
Аза решал следующию задачу от Нархана: Вам задан массив $a$, состоящий из $n$ целых неотрицательных чисел. Назовем разделение массива $a$ на $k$ отрезков $(l_1, r_1), \ldots, (l_k, r_k)$ $x$- хорошим, если выполняются следующие условия:
- Каждый элемент массива $a$ принадлежит ровно одному отрезку.
- Для каждого $1 <= i <= k$, $MEX$ чисел $(a_{l_i}, \ldots, a_{r_i})$ был меньше или равен $x$.
- $MEX$ для $[2,2,1]$ равен $0$, поскольку $0$ не принадлежит массиву.
- $MEX$ для $[3,1,0,1]$ равен $2$, поскольку $0$ и $1$ принадлежат массиву, а $2$ — нет.
- $MEX$ для $[0,3,1,2]$ равен $4$, поскольку $0$, $1$, $2$ и $3$ принадлежат массиву, а $4$ — нет.
Формат входного файла
Первая строка содержит одно целое число — $n$ ($1 <= n <= 10^6$).
Вторая строка содержит $n$ целых чисел $a_1, a_2, \ldots, a_n$ $(0 <= a_i <= 10^6)$ — массив $a$.
Формат выходного файла
Выведите $n$ целых чисел, где $i$-е число — это минимальный возможный размер $x$ хорошего разделения при $x = i-1$, если данное разделение невыполнимо выведите $-1$.
Примеры:
Вход 4 0 1 0 2Ответ
-1 3 2 1Вход
1 2Ответ
1
Замечание
В первом примере:
- при $x = 0$, не существует хорошего разделения массива, поэтому выводим $-1$.
- при $x = 1$, делим на $3$ отрезка: [$0$],[$1$],[$0,2$].
- при $x = 2$, делим на $2$ отрезка: [$0,1$], [$0,2$].
- при $x = 3$, один отрезок - сам массив [$0,1,0,2$].
комментарий/решение(4) Проверить мое решение
Задача C. Запросы на перестановке
Ограничение по времени:
1.5 секунд
Ограничение по памяти:
256 мегабайт
У вас есть перестановка $p_1, \ldots, p_n$ и массив целых чисел $a_1, \ldots, a_n$, который изначально заполнен нулями. Вам нужно обработать $q$ запросов одного из трёх типов:
- $1 l r x$: для всех $l <= i <= r$, добавить $x$ к $a_{p_i}$.
- $2 l r$: вычислить и вывести $a_l + a_{l+1} + \cdots + a_r$.
- $3 a b$: поменять местами $p_a$ и $p_b$.
Формат входного файла
В первой строке записаны два целых числа $n$ и $q$ ($2 <= n, q <= 10^5$) — размер перестановки и количество запросов.
Во второй строке записаны $n$ целых чисел $p_1, \ldots, p_n$ ($1 <= p_i <= n$, $p_i \neq p_j$ если $i \neq j$).
Каждая из следующих $q$ строк содержат описания запросов
Каждый запрос задан в одном из следующих форматов в зависимости от типа запроса:
$1 l r x$ ($1 <= l <= r <= n$, $1 <= x <= 10^5$) для запросов первого типа.
$2 l r$ ($1 <= l <= r <= n$) для запросов второго типа.
$3 a b$ ($1 <= a, b <= n$, $a \neq b$) для запросов третьего типа.
Формат выходного файла
Выведите ответы на все запросы второго типа, каждый ответ в отдельной строке.
Пример:
Вход 6 9 4 6 3 1 2 5 1 4 5 3 3 3 5 1 2 3 6 3 3 6 3 2 1 2 1 5 2 1 6 1 1 5 6 2 4 6Ответ
12 18 24
комментарий/решение(2) Проверить мое решение
Задача D. Витя - черепашка ниндзя 2
Ограничение по времени:
1 секунда
Ограничение по памяти:
256 мегабайт
Дается прямоугольная таблица $N \times M$, в каждой клетке записано какое-то число. Витя находится в левой верхней клетке, его цель добраться до правого нижнего угла. За один ход ему разрешается перемещаться в соседнюю клетку либо вправо, либо вниз (влево и вверх перемещаться запрещено). За посещение клетки, Витя должен платить число указанное в этой клетке. Дончик владелец таблицы. Он решил сделать скидку своему другу Вите, разрешив платить только за самые дорогие(наибольшие по значению) $K$ клеток на его пути от левого верхнего угла в правый нижний. Какое минимальное количество денег потратит Витя для достижения своей цели?
Формат входного файла
В первой строке даны три целых числа $N,M$ и $K$ ($1 <= N, M <= 500$, $1 <= K <= N + M - 1$).
В следующих $N$ строках даны по $M$ целых чисел — $j$-е число на $i$-й строке $a_{i, j}$ ($0 <= a_{i, j} <= 500$) является числом на клетке в $i$-й строке и $j$-м столбце таблицы.
Формат выходного файла
Выведите одно целое число — ответ на задачу.
Примеры:
Вход 3 3 5 1 1 1 6 6 10 1 7 3Ответ
16Вход
4 4 2 1 3 2 6 7 4 5 2 1 4 6 7 1 0 1 0Ответ
8
Замечание
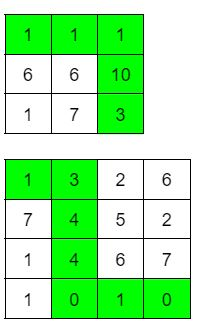
комментарий/решение(1) Проверить мое решение
Задача E. Шоколадки
Ограничение по времени:
2.5 секунд
Ограничение по памяти:
256 мегабайт
Айбар и Данияр решили купить шоколадки перед олимпиадой. Допустим, в магазине продаются $n$ видов шоколадок пронумерованных от $1$ до $n$. У каждого вида шоколадки $i$ есть свой уровень сладости $a_i$. Айбар и Данияр договорились покупать шоколадки по следующей нехитрой схеме:
- Сперва Айбар купит шоколадку с самой большой сладостью. Затем Данияр тоже купит шоколадку с самой большой сладостью среди других видов шоколадок. Более формально, если Айбар купил шоколадку вида $i$, Данияр должен купить шоколадку вида $j \neq i$ такую, что её сладость самая большая.
- Теперь Айбар купит шоколадку с самой маленькой сладостью. Затем Данияр тоже купит шоколадку с самой маленькой сладостью среди других видов шоколадок. Более формально, если Айбар купил шоколадку вида $i$, Данияр должен купить шоколадку вида $j \neq i$ такую, что её сладость самая маленькая.
Формат входного файла
В первой строке дано одно целое число $n$ — количество видов шоколадок в супермаркете ($2 <= n <= 250000$).
Во второй строке даны $n$ чисел $b_1, \ldots, b_n$ ($1 <= b_i <= 10^9$).
Формат выходного файла
Выведите одно целое число — количество искомых пар.
Примеры:
Вход 3 1 2 3Ответ
3Вход
5 1 1 3 2 1Ответ
6
Замечание
Во втором примере, подходят следующие пары: $(1, 2), (2, 3), (2, 4), (3, 4), (3, 5), (4, 5)$
комментарий/решение Проверить мое решение
Задача F. Нархан и скобочки
Ограничение по времени:
1.5 секунд
Ограничение по памяти:
256 мегабайт
Недавно на уроке информатики Нархан проходил скобочные последовательности. После этого он захотел придумать обозначение $k$-особенной скобочной последовательности. Давайте рассмотрим скобочную последовательность длины $n$, где $n$ - четное. Нархан сперва выбрал для каждого индекса особенная она или нет. Теперь он считает скобочную последовательность $k$-особенной, если на особенных индексах стоят ровно $k$ открывающихся скобок и сама последовательность является правильной скобочной последовательностью. Также он хочет определить красоту этой скобочной последовательности и для этого у него есть массив из $n$ положительных целых чисел $a_1, a_2, \dots a_n$. Давайте выпишем все индексы $k$-особенной скобочной последовательности где стоят открывающиеся скобки, пусть это $i_1, i_2, \dots, i_m$. Тогда красотой этой последовательности для Нархана будет - $a_{i_1} + a_{i_2} + \dots + a_{i_m}$. Вам известны числа $n$ и $k$, массив $a_1, a_2, \dots a_n$, а также какие позиции особенные. Помогите Нархану найти среди всех $k$-особенных скобочных последовательностей максимальную возможную красоту, так как эта задача для него является непосильной. Определение правильной скобочной последовательности смотрите в примечаниях.
Формат входного файла
Первая строка содержит два целых числа - $n$ и $k$ ($2 <= n <= 2*10^5, 0 <= k <= n$) . Гарантируется, что $n$ - четное.
Во второй строке $n$ целых числа $a_1, \ldots, a_n$ ($1 <= a_i <= 10^9$) - значения элементов массива.
В третьей строке $n$ чисел $c_1, \ldots, c_n$ $(c_i = \{0, 1\})$. $c_i=1$ означает, что индекс $i$ - особенный, иначе нет.
Формат выходного файла
Если нет ни одной $k$-особенной скобочной последовательности длины $n$ выведите $-1$. Иначе выведите максимальную красоту среди всех $k$-особенных скобочных последовательностей
Примеры:
Вход 6 3 1 6 3 4 7 3 1 1 1 1 1 1Ответ
14Вход
6 0 1 2 3 4 5 6 1 0 0 0 0 0Ответ
-1Вход
8 3 7 9 12 5 6 6 8 9 0 1 1 0 1 1 1 0Ответ
36
Замечание
Напомним, что такое правильная скобочная последовательность:
- <<()>> — правильная скобочная последовательность;
- если $s$ — правильная скобочная последовательность, то <<(>> + $s$ + <<)>> — правильная скобочная последовательность;
- если $s$ и $t$ — правильные скобочные последовательности, то $s + t$ — правильная скобочная последовательность.
комментарий/решение Проверить мое решение