4-й этап Республиканской олимпиады по информатике 2021-2022, 2 тура
Есеп A. Қосындымен бояу
Ограничение по времени:
1 second
Ограничение по памяти:
256 megabytes
Сізде $n$ бүтін саннан тұратын $a_1, \ldots, a_n$ массиві бар. Бастапқыда массивтегі әрбір сан ақ түске боялған. Бір операцияда сіз:
- Үш $(a_i, a_j, a_k)$ ақ санды таңдайсыз ($1 <= i, j, k <= n$, $i \neq j$, $i \neq k$, $j \neq k$).
- Егер $a_i + a_j$ мәні $a_k$ мәнінен үлкен болса, $a_k$ санын қара түске бояйсыз.
Формат входного файла
Бірінші жолда бір бүтін $n$ саны — массив өлшемі бар ($3 <= n <= 10^5$).
Екінші жолда $n$ бүтін сан $a_1, \ldots, a_n$ ($-10^9 <= a_i <= 10^9$) бар.
Формат выходного файла
Бір бүтін санды басып шығарыңыз — мүмкін соңғы бояулар саны. Берілген шектеулер бойынша жауап ешқашан $10^{18}$ мәнінен аспайтынын көрсетуге болады.
Примеры:
Вход 3 2 2 5Ответ
2Вход
4 -3 1 2 2Ответ
3
комментарий/решение(2) шыгару
Есеп В. MEXI
Ограничение по времени:
1.5 seconds
Ограничение по памяти:
512 megabytes
Нархан Аза-ға келесі есепті ұсынды: Сізге мөлшері $n$ болатын бүтін сандардан тұратын $a$ массиві берілген. $a$ массивін $k$ бөлікке $(l_1, r_1), \ldots, (l_k, r_k)$ бөлуін $x$-жақсы бөлініс деп атаймыз егер келесі шарттар орындалса:
- $a$ массивының кез-келген элементі дәл бір бөлікте жатады.
- Кез келген $1 <= i <= k$ үшін, $(a_{l_i}, \ldots, a_{r_i})$ сандарының $MEX$і $x$-тен кіші немесе тең болады.
- $[2,2,1]$ $MEX$i $0$, себебі $0$ массивте кездеспейді.
- $[3,1,0,1]$ $MEX$і $2$, себебі $0$ жәңе $1$ массивте кездеседі, ал $2$ — жоқ.
- $[0,3,1,2]$ $MEX$і $4$, себебі $0$, $1$, $2$ жәңе $3$ массивте кездеседі, ал $4$ — жоқ.
Формат входного файла
Бірінші жолда бір бүтін сан — $n$ ($1 <= n <= 10^6$) берілген.
Екінші жолда $n$ бүтін сандар $a_1, a_2, \ldots, a_n$ $(0 <= a_i <= 10^6)$ — $a$ массиві берілген.
Формат выходного файла
$n$ бүтін санды шығарыңыз, мұнда $i$-ші сан ол $x = i-1$ кездегі ең кішкентай мүмкін болатың $x$ жақсы бөліністің өлшемі. Олай бөлу мүмкін болмаса $-1$ шығарыңыз.
Примеры:
Вход 4 0 1 0 2Ответ
-1 3 2 1Вход
1 2Ответ
1
Замечание
Бірінші мысалда:
- $x = 0$ болғанда, жақсы бөлініс жоқ, сол себепті $-1$ шығарамыз.
- $x = 1$ болғанда, $3$ бөлікке бөлеміз: [$0$],[$1$],[$0,2$].
- $x = 2$ болғанда, $2$ бөлікке бөлеміз: [$0,1$], [$0,2$].
- $x = 3$ болғанда, бір бөлік массивтың өзі [$0,1,0,2$].
комментарий/решение(4) шыгару
Есеп С. Ауыстырмадағы сұраныстар
Ограничение по времени:
1.5 seconds
Ограничение по памяти:
256 megabytes
Сізге $p_1, \ldots, p_n$ ауыстырмасы және $a_1, \ldots, a_n$ бүтін сандар массиві берілген. Сізге 3 түрлі $q$ сұраныстарды орындау керек:
- $1 l r x$: әр $l <= i <= r$ үшін, $x$-ты $a_{p_i}$-ға қосу.
- $2 l r$: $a_l + a_{l+1} + \cdots + a_r$ мәнін есептеу және шығару.
- $3 a b$: $p_a$ және $p_b$ орындарын ауыстыру.
Формат входного файла
Бірінші жолда $n$ және $q$ екі бүтін саны жазылған($2 <= n, q <= 10^5$) — ауыстырманың мөлшері мен сұраныстар саны.
Екінші жолда $n$ бүтін сан $p_1, \ldots, p_n$ ($1 <= p_i <= n$, $p_i \neq p_j$ егер $i \neq j$) жазылған.
Келесі $q$ жолда сұраныстардың сипаттамасы берілген.
Әр сұраныс түріне байланысты келесі форматтардың бірінде берілген:
$1 l r x$ ($1 <= l <= r <= n$, $1 <= x <= 10^5$) бірінші түрдің сұраныстары үшін.
$2 l r$ ($1 <= l <= r <= n$) екінші түрдің сұраныстары үшін.
$3 a b$ ($1 <= a, b <= n$, $a \neq b$) үшінші түрдің сұраныстары үшін.
Формат выходного файла
Әр екінші түрдің сұранысы үшін бөлек жолда есептің жауабын шығарыңыз.
Пример:
Вход 6 9 4 6 3 1 2 5 1 4 5 3 3 3 5 1 2 3 6 3 3 6 3 2 1 2 1 5 2 1 6 1 1 5 6 2 4 6Ответ
12 18 24
комментарий/решение(2) шыгару
Есеп D. Витя - тасбақа-ниндзя 2
Ограничение по времени:
1 second
Ограничение по памяти:
256 megabytes
Әр торында бір сан жазылған $N \times M$ кестесі беріледі. Витя сол жақ жоғарғы торда орналасқан, оның мақсаты-төменгі оң жақ бұрышқа жету. Бір қадамда оған көрші торға оңға немесе төменге (солға және жоғарыға жылжуға тыйым салынады) өтуге рұқсат етіледі. Торда болғаны үшін Витя осы торда көрсетілген санды төлеуі керек. Дончик кестенің иесі. Ол өзінің досы Витяға жеңілдік жасауға шешім қабылдады - сол жақ жоғарғы бұрыштан төменгі оң жаққа дейінгі жолда ең қымбат(ең үлкен сан жазылған) $K$ торға ғана төлеуге рұқсат берді. Витя өз мақсатына жету үшін ең аз дегенде қанша ақша жұмсайды?
Формат входного файла
Бірінші жолда үш бүтін сан $N,M$ және $K$ ($1 <= N, M <= 500$, $1 <= K <= N + M - 1$) беріледі.
Келесі $N$ жолда $M$ саннан беріледі — $i$-ші жолдағы $j$-ші сан $a_{i, j}$ ($0 <= a_{i, j} <= 500$) $i$-ші жолда және $j$-ші бағанда жазылған сан.
Формат выходного файла
Жалғыз бүтін сан — есеп жауабың шығарыңыз.
Примеры:
Вход 3 3 5 1 1 1 6 6 10 1 7 3Ответ
16Вход
4 4 2 1 3 2 6 7 4 5 2 1 4 6 7 1 0 1 0Ответ
8
Замечание
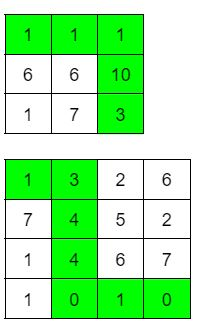
комментарий/решение(1) шыгару
Есеп E. Шоколадтар
Ограничение по времени:
2.5 seconds
Ограничение по памяти:
256 megabytes
Айбар мен Данияр олимпиада алдында шоколад сатып алуды шешті. Дүкенде $1$-ден $n$-ға дейін нөмірленген шоколадтардың $n$ түрі сатылады делік. Шоколадтың $i$-нші түрінде $a_i$ тәттілік деңгейі бар. Айбар мен Данияр келесі қарапайым схема бойынша шоколад сатып алуға келісті:
- Алдымен Айбар ең тәтті шоколадты сатып алады. Сонда Данияр да шоколадтың басқа түрлерінің ішінде ең тәтті шоколадты алады. Ресми түрде айтқанда, Айбар түрі $i$ болатын шоколадты алса, Данияр түрі $j \neq i$ болатын тәттілігі ең жоғары шоколадты сатып алуы керек.
- Енді Айбар тәттілігі ең төмен шоколадты сатып алады. Содан кейін Данияр да шоколадтың басқа түрлерінің ішінде тәттілігі ең кішкентай шоколадты сатып алады. Ресми түрде айтқанда, Айбар түрі $i$ болатын шоколадты алса, Данияр түрі $j \neq i$ болатын тәттілігі ең төмен шоколадты сатып алуы керек.
Формат входного файла
Бірінші жолда $n$ — супермаркеттегі шоколад түрлерінің саны ($2 <= n <= 250000$) бар.
Екінші жолда $n$ сандар $b_1, \ldots, b_n$ ($1 <= b_i <= 10^9$) бар.
Формат выходного файла
Бір бүтін санды басып шығарыңыз — қажетті жұптар саны.
Примеры:
Вход 3 1 2 3Ответ
3Вход
5 1 1 3 2 1Ответ
6
Замечание
Екінші мысалда келесі жұптар сәйкес келеді: $(1, 2), (2, 3), (2, 4), (3, 4), (3, 5), (4, 5)$
комментарий/решение шыгару
ЕсепF. Нархан және жақшалар
Ограничение по времени:
1.5 seconds
Ограничение по памяти:
256 megabytes
Нархан информатика сабағында жақшалар тізбегін өтті. Осыдан кейін, оған керемет ой келді: $k$-ерекше жақшалар тізбегін ойлап табу. Ұзындығы $n$ болатын жақшалар тізбегін қарастырайық, мұнда $n$ жұп сан. Нархан алдымен әр индекс үшін ерекше немесе жоқ екенін анықтайды. Енді ол жақшалар тізбегін $k$-ерекше деп санайды, егер тізбек дұрыс болса және ерекше индекстерде дәл $k$ ашылатын жақша тұрса. Сондай-ақ, ол осы жақшалар тізбегінің әсемдігін санағысы келеді. Санау үшін, ол $n$ оң бүтін саннан тұратын, $a_1, a_2, \dots a_n$ массивын алады. Егер $k$-ерекше жақшалар тізбегінде $i_1, i_2, \dots, i_m$, ашылатын жақшалар тұрған индекстар болса, тізбектің әсемдігі - $a_{i_1} + a_{i_2} + \dots + a_{i_m}$ болады. Сіз $n$, $k$ сандарын және $a_1, a_2, \dots a_n$ массивын білесіз. Сондай-ақ қандай индекстар ерекше екені белгілі. Нарханға бүкіл $k$-ерекше жақшалар тізбегінің ішінен, ең үлкен әсемдікті табуға көмектесіңіз. Дұрыс жақшалар тізбегінің анықтамасы ескертулерде жазылған.
Формат входного файла
Бірінші жолда екі, $n$ және $k$, бүтін сандары бар. ($2 <= n <= 2*10^5, 0 <= k <= n$) $n$ жұп болатынына кепілдік беріледі.
Екінші жолда $n$ бүтін сан $a_1, \ldots, a_n$ ($1 <= a_i <= 10^9$) бар.
Үшінші жолда $n$ бүтін сан $c_1, \ldots, c_n$ $(c_i = \{0, 1\})$ бар. $c_i=1$ - $i$-индекс ерекше екенін білдіреді, әйтпесе жоқ.
Формат выходного файла
Ұзындығы $n$ болатын $k$-ерекше жақшалар тізбегі болмаса, $-1$ шығарыңыз. Әйтпесе, барлық $k$-ерекше жақшалар тізбектерінің арасында ең үлкен әсемдікті шығарыңыз.
Примеры:
Вход 6 3 1 6 3 4 7 3 1 1 1 1 1 1Ответ
14Вход
6 0 1 2 3 4 5 6 1 0 0 0 0 0Ответ
-1Вход
8 3 7 9 12 5 6 6 8 9 0 1 1 0 1 1 1 0Ответ
36
Замечание
Дұрыс жақшалар тізбегінің анықтамасы:
- <<()>> — дұрыс жақшалар тізбегі;
- егер $s$ дұрыс жақшалар тізбегі болса, онда <<(>> + $s$ + <<)>> дұрыс жақшалар тізбегі болады;
- егер $s$ және $t$ дұрыс жақшалар тізбегі болса, $s + t$ дұрыс жақшалар тізбегі болады.
комментарий/решение шыгару