3-й этап Республиканской олимпиады по информатике 2022-2023, 2й тур
Задача D. Две очереди
Ограничение по времени:
1 секунда
Ограничение по памяти:
256 мегабайт
Есть две очереди. В первой стоят $n$ людей, во второй стоят $m$ людей. В первой очереди обслуживают одного человека за $A$ минут, во второй очереди обслуживают одного человека за $B$ минут. Отсчет времени начинается с минуты $1$. Каждую минуту последовательно происходит следующее:
- Если первый человек в первой очереди обслужен, то он уходит из очереди.
- Если первый человек во второй очереди обслужен, то он уходит из очереди.
- Последний человек в первой очереди перемещается в конец второй очереди если его порядковый номер во второй очереди окажется меньше чем его номер в первой очереди.
- Последний человек во второй очереди перемещается в конец первой очереди если его порядковый номер в первой очереди окажется меньше чем его номер во второй очереди.
Формат входного файла
В первой и единственной строке входного файла даны четыре целых числа $n$, $m$, $A$ и $B$ ($1 <= n, m, A, B <= 10^5$).
Формат выходного файла
Выведите одно целое число — первый момент времени $T$ когда все люди будут обслужены.
Примеры:
Вход 2 3 1 2Ответ
4Вход
5 6 4 4Ответ
24Вход
3 1 2 4Ответ
8
Замечание
Разберем первый пример.
Минута $1$. Первый человек из первой очереди обслужен и уходит из очереди. Теперь $n=1$, $m=3$. Последний человек во второй очереди переходит в конец первой очереди. Теперь $n=2$, $m=2$.
Минута $2$. Первый человек из первой очереди обслужен и уходит из очереди. Теперь $n=1$, $m=2$. Первый человек из второй очереди обслужен и уходит из очереди. Теперь $n=1$, $m=1$. Больше ничего не происходит.
Минута $3$. Первый человек из первой очереди обслужен и уходит из очереди. Теперь $n=0$, $m=1$. Больше ничего не происходит.
Минута $4$. Первый человек из второй очереди обслужен и уходит из очереди. Теперь $n=0$, $m=0$. Все люди обслужены, значит ответ $T=4$.
комментарий/решение Проверить мое решение
Задача E. Покраска графа
Ограничение по времени:
1 секунда
Ограничение по памяти:
256 мегабайт
Дан ориентированный ацикличный граф из $N$ вершин и $M$ ребер. Вершины пронумерованы целыми числами от $1$ до $N$. Причем в графе нет ребра из вершины $1$ в вершину $N$. Все вершины изначального белого цвета. Мансуру нужно покрасить ровно $B$ вершин в черный цвет. После покраски удаляются все ребра у которых оба конца одного цвета. Помогите Мансуру покрасить $B$ вершин таким образом, чтобы нельзя было добраться из $1$ в $N$ после удаления всех ребер у которых оба конца одного цвета.
Формат входного файла
Каждый тест содержит несколько наборов входных данных.
Первая строка содержит одно целое число $T$($1 <= T <= 100$) — количество входных данных.
Первая строка каждого набора входных данных содержит три целых числа $N$,$M$ и $B$($3 <= N <= 10^5$, $0 <= M <= min(2 \cdot 10^5,\frac{N \cdot (N - 1)}{2})$, $1 <= B <= N$). Следующие $M$ строк каждого набора входных данных содержат по два целых числа $u$ и $v$($1 <= u, v <= N$, $u \ne v$, $(u,v) \ne (1, N)$) — задающие ориентированное ребро из вершины $u$ в вершину $v$. Гарантируется, что в графе нет цикл и повторяющихся ребер.
Cумма $N$ по всем наборам входных данных не превосходит $10^6$.
Cумма $M$ по всем наборам входных данных не превосходит $10^6$.
Формат выходного файла
Если невозможно покрасить нужным образом, выведите <<-1>>.
Иначе, выведите $B$ различных целых числа — номера вершин которые нужно покрасить в черный цвет. Если есть несколько возможных ответов, выведите любую из них.
Пример:
Вход 2 15 16 5 1 2 1 3 1 4 1 5 2 7 3 7 4 8 5 7 7 9 8 9 9 10 9 11 9 12 10 15 11 15 12 15 3 2 2 2 3 1 2Ответ
1 8 10 7 9 2 3
Замечание
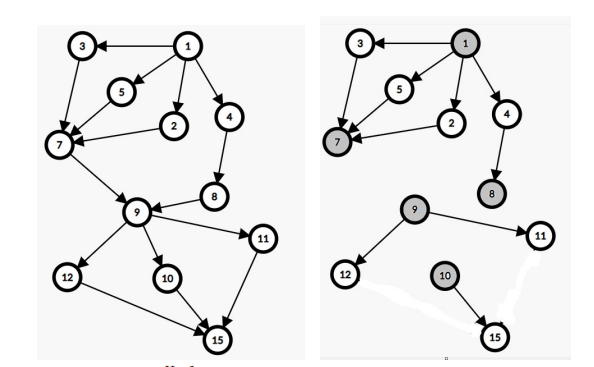
комментарий/решение Проверить мое решение
Задача F. XOR-сумма
Ограничение по времени:
2 секунды
Ограничение по памяти:
512 мегабайт
Дан массив $a$ из $n$ целых положительных чисел. Для каждого целого числа $k$ от $1$ до $m$ найдите значение $(a_1 \bmod k) \oplus (a_2 \bmod k) \oplus \ldots \oplus (a_n \bmod k)$. Здесь $\oplus$ обозначает операцию побитового XOR или исключающего ИЛИ. Данная операция существует во всех современных языках программирования, например, в языках C++,Python и Java она обозначена как <<^>>, в Pascal — как <
Формат входного файла
В первой строке задаются два целых числа $n$ и $m$ ($1 <= n, m <= 500\,000$).
Во второй строке задаются массив $a_1, a_2, \ldots, a_n$ ($1 <= a_i <= m$).
Формат выходного файла
Выведите $m$ целых чисел через пробел, где $k$-е число равно значению $(a_1 \bmod k) \oplus (a_2 \bmod k) \oplus \ldots \oplus (a_n \bmod k)$.
Примеры:
Вход 4 5 2 5 4 2Ответ
0 1 3 1 4Вход
10 12 1 2 4 8 9 10 11 12 3 5Ответ
0 1 1 1 0 1 0 5 9 3 11 1
комментарий/решение Проверить мое решение