3-й этап Республиканской олимпиады по информатике 2020-2021, 2 тура
Задача B. Тетрис
Ограничение по времени:
1 секунда
Ограничение по памяти:
256 мегабайт
BThero играет в тетрис. Поле можно представить как прямоугольник с шириной $W$ и бесконечной высотой. Для удобства скажем что прямоугольник находится на двумерной системе координат. Левая нижняя клетка поля имеет координаты $(1, 1)$, а правая нижняя — $(W, 1)$. В игре последовательно произошли $q$ событий двух типов:
- На поле падает новый прямоугольник покрывающий $x$-отрезок $[l,r]$ и высотой $h$. Он начинает падать с бесконечной высоты и падает до тех пор, пока не уткнется в другой прямоугольник или на дно поля. Заметьте, что в данной вариации тетриса двигать прямоугольники вы не можете.
- Поступает запрос с одним целым числом $y$. Надо ответить, сколько клеток на высоте $y$ уже заняты прямоугольниками.
Формат входного файла
В первой строке даны два целых числа $W$ и $q$ ($1 <= W <= 10^6$, $2 <= q <= 10^5$).
В последующих $q$ строках идут описания событий. Сперва дается одно целое число $t$ — тип события. Если $t = 1$, это событие первого типа и вам дополнительно даются три целых числа $l$, $r$ и $h$ ($1 <= l <= r <= W$, $1 <= h <= 10^6$). Если $t = 2$, это событие второго типа и вам дополнительно дается одно целое число $y$ ($1 <= y <= 10^9$).
Гарантируется, что есть хотя бы одно событие первого типа и хотя бы одно событие второго типа.
Формат выходного файла
Выходной файл должен содержать ответы на все события второго типа.
Система оценки
Данная задача содержит $6$ подзадач, в которых выполняются следующие ограничения:
- $q <= 5000$. Оценивается в $20$ баллов.
- Гарантируется, что самое первое событие первого типа, а все последующие — второго типа. Оценивается в $10$ баллов.
- Гарантируется, что все прямоугольники имеют высоту $1$, ширину $1$ и для всех событий второго типа $y <= 10^6$. Оценивается в $10$ баллов.
- Гарантируется, что все прямоугольники имеют ширину $1$ и для всех событий второго типа $y <= 10^6$. Оценивается в $20$ баллов.
- Для всех событий второго типа $y <= 10^6$. Оценивается в $20$ баллов.
- Исходные условия задачи. Оценивается в $20$ баллов.
Пример:
Вход 13 10 1 7 11 4 2 3 1 4 9 2 2 3 2 5 1 1 3 5 2 5 1 2 4 1 2 6 2 7Ответ
5 5 6 9 6 3
Замечание
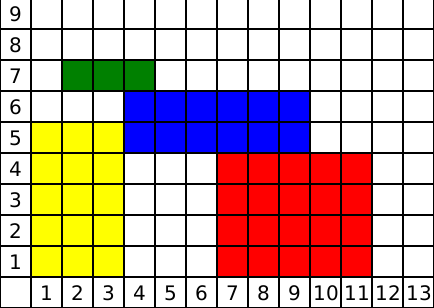
Комментарий/решение:
Возможно, что при неправильном наборе формул, они будут
доредактированы модератором. При этом содержание не будет меняться.