3-й этап Республиканской олимпиады по информатике 2020-2021, 2 тура
Задача A. Матрицы
Ограничение по времени:
1 секунда
Ограничение по памяти:
256 мегабайт
Вам дана матрица размера $N \times M$, состоящая из целых положительных чисел, а также целое число $K$. Назовем подматрицу хорошей, если она является квадратом и сумма этой подматрицы не больше $K$. Посчитайте количество хороших подматриц. Подматрицей называется такая матрица, которую можно получить из исходной, если удалить из нее несколько(возможно ноль) столбцов с левого и правого края, а также несколько(возможно ноль) строк с верхнего и нижнего края. При этом подматрица не должна быть пустой.
Формат входного файла
В первой строке заданы $3$ целых числа $N$, $M$, $K$ — размеры матрицы и ограничение на сумму. ($1 <= N, M <= 1500$, $0 <= K <= 10^9$)
В следующих $N$ строках содержится по $M$ целых положительных чисел — содержимое матрицы (числа по значению от $1$ до $1000$).
Формат выходного файла
Выведите одно число — количество подходящих подматриц.
Система оценки
Данная задача содержит $6$ подзадач, в которых выполняются следующие ограничения:
- Тесты из условия. Оценивается в $0$ баллов.
- $N, M <= 2$. Оценивается в $15$ баллов.
- $N, M <= 100$. Оценивается в $17$ баллов.
- $N, M <= 500$. Оценивается в $24$ балла.
- $N, M <= 1500$ и матрица состоит только из единичек. Оценивается в $15$ баллов.
- Исходные ограничения. Оценивается в $29$ баллов.
Примеры:
Вход 3 3 12 1 2 3 5 2 5 3 2 4Ответ
12Вход
6 6 30 4 4 4 1 1 1 2 5 5 3 2 3 3 2 2 4 1 3 1 1 4 4 4 5 1 3 3 4 5 5 2 5 5 4 3 4Ответ
71
комментарий/решение(2) Проверить мое решение
Задача B. AB
Ограничение по времени:
1 секунда
Ограничение по памяти:
256 мегабайт
Вам даны две строки $s$ и $t$, которые состоят из букв 'a' и 'b'. В строке $s$ нет соседних одинаковых букв. Вы хотите выбрать наибольшее количество непересекающихся подпоследовательностей $t$, которые равны $s$. Подпоследовательность — это такая последовательность строки, которая может быть получена удалением нескольких (возможно ноль) элементов из этой строки. Найдите максимальное количество подпоследовательностей, которое вы сможете выбрать.
Формат входного файла
Первая строка входных данных содержит одну строку s ($1 <= |s| <= 4$). Гарантируется, что в строке $s$ нет соседних одинаковых букв.
Вторая строка входных данных содержит одну строку t ($1 <= |t| <= 10^5$).
Формат выходного файла
Выведите одно целое число — максимальное количество подпоследовательностей, которое вы сможете выбрать.
Система оценки
Данная задача содержит $7$ подзадач, в которых выполняются следующие ограничения:
- Тесты из условия. Оценивается в $0$ баллов.
- $|s| = 1$. Оценивается в $11$ баллов.
- $|s| = 2$. Оценивается в $14$ баллов.
- $|s| = 3$. Оценивается в $20$ баллов.
- $|s| = 4$, $|t| <= 50$. Оценивается в $18$ баллов.
- $|s| = 4$, $|t| <= 300$. Оценивается в $12$ баллов.
- $|s| = 4$, $|t| <= 10^5$. Оценивается в $25$ баллов.
Примеры:
Вход ab abbabaОтвет
2Вход
aba ababaaОтвет
2
Замечание
Во втором примере можно выбрать две непересекающихся последовательности c индексами {1, 2, 5} и {3, 4, 6}.
комментарий/решение(1) Проверить мое решение
Задача C. Разделяем на пары
Ограничение по времени:
1 секунда
Ограничение по памяти:
256 мегабайт
Есть массив $a$ из $n$ целых чисел. Для каждого $k$ от 1 до $\lfloor \frac{n}{2} \rfloor$, найдите $k$ различных пар, что сумма абсолютных разностей пар была минимизирована. Более формально, выберите $2k$ различных индексов, и разбейте их на $k$ пар $(i_1, j_1), (i_2, j_2), \dots, (i_k, j_k)$, чтобы значение $|a_{i_1} - a_{j_1}| + |a_{i_2} - a_{j_2}| + \dots + |a_{i_k} - a_{j_k}|$ было минимально.
Формат входного файла
В первой строке находятся одно целое число $n$ ($1 <= n <= 2*10^5$).
Во второй строке находятся $n$ целых чисел $a_1, a_2,…, a_n (1 <= a_i <= 10^9)$.
Формат выходного файла
Выведите $\lfloor \frac{n}{2} \rfloor$ целых чисел, где $k$-е число является ответом $k$ пар.
Система оценки
Данная задача содержит $6$ подзадач, в которых выполняются следующие ограничения:
- $n <= 11$. Оценивается в $7$ баллов.
- $n <= 18$. Оценивается в $11$ баллов.
- $n <= 500$. Оценивается в $13$ баллов.
- $n <= 5000$. Оценивается в $15$ баллов.
- $a_i <= 5000$. Оценивается в $13$ баллов.
- Исходные условия задачи. Оценивается в $41$ баллов.
Примеры:
Вход 6 1 3 5 8 13 21Ответ
2 5 13Вход
11 31 12 1 36 41 57 21 79 86 63 97Ответ
5 11 18 27 39
комментарий/решение Проверить мое решение
Задача A. Разделение команды
Ограничение по времени:
1 секунда
Ограничение по памяти:
256 мегабайт
Есть $n$ игроков которые стоят в ряд. Они хотят сыграть в игру. Для этого им нужно разделится на две команды по $k$ человек. У $i$-го игрока $a_i$ уровень игры. Сила команды это сумма уровней всех его участников. Вы можете выбрать $2 * k$ игроков которые будут играть. Но они сами поделятся на команды. В первой команде будут первые $k$ игроков которые стоят ближе к началу ряду. Во второй команде будут последние $k$ игроков. Запишем силу первой команды как $A$ и второй как $B$. Найдите максимальное значение $A - B$. Например, есть $6$ игроков с уровнями $[3, 1, 7, 2, 1, 2]$. Если выбрать игроков с номерами $1, 3, 5 ,6$ то в первой команде будут игроки $1, 3$ и сила команды $A = 3 + 7 = 10$, во второй игроки $5, 6$ и сила команды $B = 1 + 2 = 3$. $A - B = 10 - 3 = 7$.
Формат входного файла
В первой строке два целых числа $n$, $k$ ($1 <= n <= 10^5$, $1 <= k <= \frac{n}{2}$) - колчество игроков и размер команд.
Во второй строке $n$ целых чисел $a_1, a_2 \ldots a_n$ ($1 <= a_i <= 10^5$) - уровень игроков.
Формат выходного файла
Выведите максимальное значение $A - B$.
Система оценки
Данная задача содержит $7$ подзадач, в которых выполняются следующие ограничения:
- $n <= 15$. Оценивается в $12$ баллов.
- $a_i \geq a_{i+1}$ для $1 <= i <= n - 1$. Оценивается в $11$ баллов.
- $a_i <= a_{i+1}$ для $1 <= i <= n - 1$. Оценивается в $11$ баллов.
- $k = 1$. Оценивается в $16$ баллов.
- $k <= 100$. Оценивается в $19$ баллов. Необходимые подзадачи: 4.
- Исходные условия задачи. Оценивается в $31$ баллов. Необходимые подзадачи: 1,2,3,4,5.
Примеры:
Вход 6 2 3 1 7 2 1 2Ответ
7Вход
5 1 3 4 6 8 9Ответ
-1
комментарий/решение(1) Проверить мое решение
Задача B. Тетрис
Ограничение по времени:
1 секунда
Ограничение по памяти:
256 мегабайт
BThero играет в тетрис. Поле можно представить как прямоугольник с шириной $W$ и бесконечной высотой. Для удобства скажем что прямоугольник находится на двумерной системе координат. Левая нижняя клетка поля имеет координаты $(1, 1)$, а правая нижняя — $(W, 1)$. В игре последовательно произошли $q$ событий двух типов:
- На поле падает новый прямоугольник покрывающий $x$-отрезок $[l,r]$ и высотой $h$. Он начинает падать с бесконечной высоты и падает до тех пор, пока не уткнется в другой прямоугольник или на дно поля. Заметьте, что в данной вариации тетриса двигать прямоугольники вы не можете.
- Поступает запрос с одним целым числом $y$. Надо ответить, сколько клеток на высоте $y$ уже заняты прямоугольниками.
Формат входного файла
В первой строке даны два целых числа $W$ и $q$ ($1 <= W <= 10^6$, $2 <= q <= 10^5$).
В последующих $q$ строках идут описания событий. Сперва дается одно целое число $t$ — тип события. Если $t = 1$, это событие первого типа и вам дополнительно даются три целых числа $l$, $r$ и $h$ ($1 <= l <= r <= W$, $1 <= h <= 10^6$). Если $t = 2$, это событие второго типа и вам дополнительно дается одно целое число $y$ ($1 <= y <= 10^9$).
Гарантируется, что есть хотя бы одно событие первого типа и хотя бы одно событие второго типа.
Формат выходного файла
Выходной файл должен содержать ответы на все события второго типа.
Система оценки
Данная задача содержит $6$ подзадач, в которых выполняются следующие ограничения:
- $q <= 5000$. Оценивается в $20$ баллов.
- Гарантируется, что самое первое событие первого типа, а все последующие — второго типа. Оценивается в $10$ баллов.
- Гарантируется, что все прямоугольники имеют высоту $1$, ширину $1$ и для всех событий второго типа $y <= 10^6$. Оценивается в $10$ баллов.
- Гарантируется, что все прямоугольники имеют ширину $1$ и для всех событий второго типа $y <= 10^6$. Оценивается в $20$ баллов.
- Для всех событий второго типа $y <= 10^6$. Оценивается в $20$ баллов.
- Исходные условия задачи. Оценивается в $20$ баллов.
Пример:
Вход 13 10 1 7 11 4 2 3 1 4 9 2 2 3 2 5 1 1 3 5 2 5 1 2 4 1 2 6 2 7Ответ
5 5 6 9 6 3
Замечание
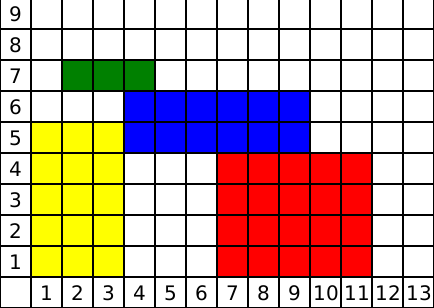
комментарий/решение Проверить мое решение
Задача C. Футболки
Ограничение по времени:
1 секунда
Ограничение по памяти:
256 мегабайт
Тима любит футболки. В городе есть очень крутой магазин футболок, который продает футболки $n$ цветов пронумерованных от $1$ до $n$, включительно. В течении $k$ дней магазин проводит масштабную акцию, где они будут продавать футболки некоторых цветов за полцены. Магазин опубликовал у себя на сайте таблицу $a$, где $a_{i,j}$ обозначает действует ли акция в $j$-й день на футболку цвета $i$ (1 если действует, иначе 0). У Тимы есть порядок предпочтений цветов $p$, который является перестановкой чисел от $1$ до $n$. Любимый цвет Тимы это цвет $p_1$, второй самый любимый это цвет $p_2$ и т.д. Каждый день в течении $k$ дней он будет приходить в магазин, и среди тех цветов на которые действует акция в тот день, он купит одну футболку с наиболее любимым цветом. Формально, в $i$-й день он выберет самый минимальный $j$, что $a_{i,{p_j}} = 1$ и купит одну футболку с цветом $p_j$. Если в тот день нет ни одного цвета, на который действует акция, то он ничего не покупает. Тима хранит $p$ в тайне. Какое максимальное количество различных цветов может оказаться среди футболок, которое он купил за $k$ дней?
Формат входного файла
В первой строке задано два целых числа $n$ и $k$ ($1 <= n <= 10^5$, $1 <= k <= 14$).
В следующих $n$ строках записано по $k$ символов — элементы $a$. Каждый символ является либо «0», либо «1».
Формат выходного файла
Выведите одно целое число — максимальное количество различных цветов, которое может оказаться среди футболок.
Система оценки
Данная задача содержит $6$ подзадач, в которых выполняются следующие ограничения:
- Тесты из условия. Оценивается в $0$ баллов.
- $n$, $k <= 2$. Оценивается в $9$ баллов.
- $n$, $k <= 8$. Оценивается в $18$ баллов.
- $n$, $k <= 14$. Оценивается в $22$ баллов.
- $n <= 10000$, $k <= 14$. Оценивается в $29$ баллов.
- Исходные условия задачи. Оценивается в $22$ баллов.
Примеры:
Вход 4 3 111 110 001 110Ответ
2Вход
3 3 000 000 000Ответ
0
комментарий/решение Проверить мое решение