Задача A. Кесте

Сізге бүтін оң сандардан тұратын $N \times M$ кестесі, сондай-ақ $K$ бүтін саны беріледі. Егер кесте шаршы болса және оның элементтерінің соммасы $K$-дан аспаса, кестені жақсы деп атайық. Жақсы ішкі кестелердің санын есептеңіз. Ішкі кесте -- егер сіз сол және оң жақ жиектен бірнеше (мүмкін нөл) бағандарды, сондай-ақ жоғарғы және төменгі жиектен бірнеше(мүмкін нөл) жолдарды алып тастасағанда пайда болатын кесте. Бұл жағдайда ішкі кесте бос болмауы керек. Бірінші жолда $3$ бүтін сандар $N$, $M$, $K$ — кестенің өлшемдері берілген . ($1 <= N, M <= 1500$, $0 <= K <= 10^9$) Келесі $N$ жолдардың әрқайсысында $M$ бүтін оң сандар — кестенің элементтері берілген ($1$-ден $1000$-ға дейінгі сандар). Бір санды — жақсы ішкі кестелердің санын шығарыңыз. Есеп $6$ бөлімнен тұрады:

1. Есептің шартында берілген тесттер. $0$ ұпайға бағаланады.
2. $N, M <= 2$. $15$ ұпайға бағаланады.
3. $N, M <= 100$. $17$ ұпайға бағаланады.
4. $N, M <= 500$. $24$ ұпайға бағаланады.
5. $N, M <= 1500$ және кестенің элементтері бірге тең. $15$ ұпайға бағаланады.
6. Есептің бастапқы шектеулері. $29$ ұпайға бағаланады.

Вход

  
3 3 12
1 2 3
5 2 5
3 2 4

Ответ

12

Вход

  
6 6 30
4 4 4 1 1 1
2 5 5 3 2 3
3 2 2 4 1 3
1 1 4 4 4 5
1 3 3 4 5 5
2 5 5 4 3 4

Ответ

71

Есеп B. AB

Сізге 'a' және 'b' әріптерінен тұратын $s$ және $t$ екі сөзі берілген. \textbf {$s$ сөзінде көрші бірдей әріптер жоқ}. Сіз $s$-ке тең $t$-ның ең көп қиылыспайтын ішкі тізбектерін таңдағыңыз келеді. Ішкі тізбек - - - бұл сөзден бірнеше (мүмкін нөл) элементтерін алып тастау арқылы алуға болатын сөз тізбегі. Таңдауға болатын ең көп ішкі тізбектердің санын табыңыз. Бірінші жолда $s$ сөзі берілген ($1 <= |s| <= 4$). $s$ cөзінде көрші бірдей әріптер жоқ екеніне кепілдік беріледі. Екінші жолда $t$ сөзі берілген ($1 <= |t| <= 10^5$). Бір бүтін санды — сіз таңдай алатын ішкі тізбектердің ең көп санын шығарыңыз. Есеп $7$ бөлімнен тұрады:

1. Есептің шартында берілген тесттер. $0$ ұпайға бағаланады.
2. $|s| = 1$. $11$ ұпайға бағаланады.
3. $|s| = 2$. $14$ ұпайға бағаланады.
4. $|s| = 3$. $20$ ұпайға бағаланады.
5. $|s| = 4$, $|t| <= 50$. $18$ ұпайға бағаланады.
6. $|s| = 4$, $|t| <= 300$. $12$ ұпайға бағаланады.
7. $|s| = 4$, $|t| <= 10^5$. $25$ ұпайға бағаланады.

Вход

ab
abbaba

Ответ

2

Вход

  
aba
ababaa

Ответ

2

Екінші мысалда {1, 2, 5} және {3, 4, 6} индекстерімен қиылыспайтын екі тізбекті таңдауға болады.

Есеп С. Жұптарға бөлеміз

$n$ бүтін сандардан тұратын $a$ массиві бар. 1-ден $\lfloor \frac{n}{2} \rfloor$-дейінгі әр $k$ үшін, жұптардың абсолютті айырмашылықтарының қосындысы минимал болатын $k$ әр түрлі жұптарды табыңыз. Басқаша айтқанда, $ |a_{i_1} - a_{j_1}| + |a_{i_2} - a_{j_2}| + \dots + |a_{i_k} - a_{j_k}|$ мәні минимал болатын, $(i_1, j_1), (i_2, j_2), \dots, (i_k, j_k)$ жұптарын табыңыз. Массивтің әр элементі ең көбі бір жұпта болуы керек. Бірінші жолда $n$ бүтін саны бар ($1 <= n <= 2 * 10^5$) - массив ұзындығы. Екінші жолда $n$ бүтін сандар берілген $a_1, a_2,..., a_n (1 <= a_i <= 10^9)$ - массив элементтері. $\lfloor \frac{n}{2} \rfloor$ бүтін сандарды шығарыңыз, мұнда $k$-саны $k$ жұпқа арналған жауап болып табылады. Бұл тапсырмада $6$ бөлікке бөлінеді:

1. $n <= 11$. $7$ баллға бағаланады.
2. $n <= 18$. $11$ баллға бағаланады.
3. $n <= 500$. $13$ баллға бағаланады.
4. $n <= 5000$. $15$ баллға бағаланады.
5. $a_i <= 5000$. $13$ баллға бағаланады.
6. мәселенің бастапқы шарттары. $ 41 $ баллға бағаланады.

Вход

6
1 3 5 8 13 21

Ответ

2 5 13

Вход

11
31 12 1 36 41 57 21 79 86 63 97

Ответ

5 11 18 27 39

Задача A. Топтық ойын

Бір күні $n$ адам ойын ойнамақшы болып шешті. Ойынды бастау үшін олар екі топқа бөлінулері керек. Әр $i$-інші ойыншының ойнау қабілеті $a_i$. Топтың күші сол топтағы ойыншылардың қабілеттерінің қосындысы. Сізге ойнайтын $2 * k$ адамды таңдау керек. Олар өзара екі топқа бөлінеді. Бірінші топта қатардың басына жақын $k$ ойыншы болады. Екінші топта қатардың соңына жақын $k$ ойыншы болады. Бірінші топтың күшін $A$, ал екінші топтың күшін $B$ деп алайық. Ең үлкен $A - B$ нәтижесін табыңыз. Мысалы, ойнау қабілеттері $[3, 1, 7, 2, 1, 2]$ болатын $6$ адам бар. Позициялары $1, 3, 5 ,6$ болатын адамдарды ойнайды деп шешсек, бірінші топта $1$-ші және $3$-ші ойыншылардан тұрады, бірінші топтың күші $A = 3 + 7 = 10$ болады. Екінші топта $5$-ші және $6$-шы ойыншылардан тұрады, екінші топтың күші $B = 1 + 2 = 3$ болады. $A - B = 10 - 3 = 7$. Бірінші жолда $n$, $k$ екі саны берілген ($1 <= n <= 10^5$, $1 <= k <= \frac{n}{2}$) - ойыншылар саны және топтың мөлшері. Екінші жолда $n$ ойыншының ойнай қабілеттері берілген $a_1, a_2 \ldots a_n$ ($1 <= a_i <= 10^5$). Ең үлкен $A - B$ мәнін табыңыз. Вход

6 2
3 1 7 2 1 2

Ответ

7

Вход

5 1
3 4 6 8 9

Ответ

-1

Бұл есеп $7$ бөліктен тұрады, әр бөліктің шектеулері төменде берілген:

1. $n <= 15$. $12$ балл береді.
2. $a_i \geq a_{i+1}$ әр $1 <= i <= n - 1$. $11$ балл береді.
3. $a_i <= a_{i+1}$ әр $1 <= i <= n - 1$. $11$ балл береді.
4. $k = 1$. $16$ балл береді.
5. $k <= 100$. $19$ балл береді. Бұл бөліктен балл алу үшін: 4-ші бөлік шығарылған болуы керек.
6. Есептің негізгі шектеулері. $31$ балл береді. Бұл бөліктен балл алу үшін: барлық 1,2,3,4,5 бөліктері шығарылған болу керек.

Есеп B. Тетрис

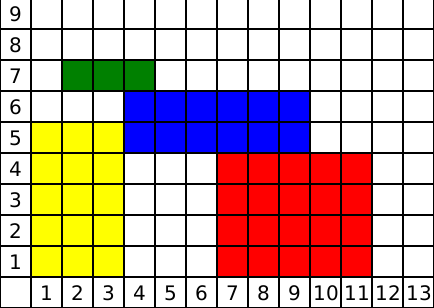
BThero тетрис ойнап отыр. Тетрис алаңың ұзындығы $W$ және биіктігі шексіз болатын тіктөртбұрыш ретінде қарастыруға болады. Ыңғайлы болу үшін алаңды жазықтықта орналастырайық. Алаңның төмендегі сол жақтағы ұяшығы $(1, 1)$ координатында, ал төмендегі оң жақтағы ұяшығы $(W, 1)$ координатасында орналасқан. Ойында кезекпен $q$ екі түрлі оқиға болды:

1. Алаңға $x$-координат бойынша $[l,r]$ кесіндісінде биіктігі $h$ болатын жаңа тіктөртбұрыш құлайды. Ол шексіз биіктіктен бастап басқа тіктөртбұрышқа тірелгенше немесе алаңның түбіне жеткенде дейін құлайды. Бұл тетрис ойынында тіктөртбұрыштарды қозғалтуға болмайды.
2. $y$ деген бүтін санмен бірге сұратым келеді. Осы $y$ биіктігінде қанша ұяшық тіктөртбұрыштардың ішінде екенін жауап беру керек.

BThero ағамызға бүкіл сұратымдарға жауап беруге көмектесіңіз! Кіріс деректердің бірінші жолында $W$ және $q$ бүтін сандары берілген ($1 <= W <= 10^6$, $2 <= q <= 10^5$). Келесі $q$ жолдарда оқиғалардың сипаттамалары берілген. Алдымен бір бүтін сан $t$ — оқиғаның түрі беріледі. Егер $t = 1$ болса, бұл бірінші түрдегі оқиға және сізге қосымша үш бүтін сан $l$, $r$ және $h$ беріледі ($1 <= l <= r <= W$, $1 <= h <= 10^6$). Егер $t = 2$ болса, бұл екінші түрдегі оқиға және сізге қосымша бір бүтін сан $y$ беріледі ($1 <= y <= 10^9$). Оқиғалар арасында кем дегенде бір бірінші түрдегі оқиға және кем дегенде бір екінші түрдегі оқиға бар. Шығыс деректерде бүкіл сұратымдардың жауаптары болу керек. Есеп $6$ бөлімнен тұрады:

1. $q <= 5000$. $20$ ұпайға бағаланады.
2. Ең бірінші оқиға бірінші түрдегі оқиға, ал бүкіл қалған оқиғалар екінші түрдегі оқиғалар. $10$ ұпайға бағаланады.
3. Бүкіл тіктөртбұрыштардың ұзындығы $1$, ені $1$ және бүкіл сұратымдарда $y <= 10^6$. $10$ ұпайға бағаланады.
4. Бүкіл тіктөртбұрыштардың ұзындығы $1$ және бүкіл сұратымдарда $y <= 10^6$. $20$ ұпайға бағаланады.
5. Бүкіл сұратымдарда $y <= 10^6$. $20$ ұпайға бағаланады.
6. Есептің толық шарттары. $20$ ұпайға бағаланады.

Вход

13 10
1 7 11 4
2 3
1 4 9 2
2 3
2 5
1 1 3 5
2 5
1 2 4 1
2 6
2 7

Ответ

5
5
6
9
6
3

Есеп C. Футболкалар

Тима футболкаларды жақсы көреді. Қалада $1$-ден $n$-ға дейін нөмірленген $n$ түсті футболкалар сататын өте керемет футболкалар дүкені бар. $k$ күн ішінде дүкен ауқымды акция өткізеді, онда олар кейбір түстердің футболкаларын жарты бағамен сатады. Дүкен өзінің веб-сайтында $a$ кестесін жариялады. Мұнда $a_{i,j}$ акция $j$-ші күні $i$-ші түсті футболкаға жарамдылығын көрсетеді (егер жарамды болса 1, әйтпесе 0). Тимада $1$-ден $n$-ға дейінгі сандарды алмаластыруы болып табылатын $p$ түстерін таңдау тәртібі бар. Тиманың сүйікті түсі - $p_1$ түсі, екінші сүйіктісі - $p_2$ түсі және т.б. Күн сайын $k$ күн ішінде ол дүкенге келіп, және сол күні акция жарамды түстердің ішінде ол ең сүйікті түсі бар бір футболка сатып алады. Басқаша айтқанда, $i $ күні ол $a_{i,{p_j}} = 1$ болатын ең төменгі $j$ таңдайды және $p_j$ түсі бар бір футболка сатып алады. Егер сол күні акцияның бір түсі болмаса, онда ол ештеңе сатып алмайды. Тима $p$ алмастыруын құпияда сақтайды. Ол $k$ күнде сатып алған футболкалар арасында әртүрлі түстердің максималды саны қандай болуы мүмкін? Бірінші жолда екі бүтін сан берілген $n$ және $k$ ($1 <= n <= 10^5$, $1 <= k <= 14$). Келесі $n$ жолдарда $k$ таңбадан — $a$ элементтері берілген. Әр таңба «0» немесе «1». Бір бүтін санды — футболкалар арасында болуы мүмкін түрлі түстердің максималды саны шығарыңыз. Есеп $6$ бөлімнен тұрады:

1. Есептің шартында берілген тесттер. $0$ ұпайға бағаланады.
2. $n$, $k <= 2$. $9$ ұпайға бағаланады.
3. $n$, $k <= 8$. $18$ ұпайға бағаланады.
4. $n$, $k <= 14$. $22$ ұпайға бағаланады.
5. $n <= 10000$, $k <= 14$. $29$ ұпайға бағаланады.
6. Есептің толық нұсқасы. $22$ ұпайға бағаланады.

Вход

4 3
111
110
001
110

Ответ

2

Вход

3 3
000
000
000

Ответ

0