Городская Жаутыковская олимпиада, 7 класс, 2008 год
Задача №1. Можно ли в клетки таблицы $n\times n$ вписать целые числа так, чтобы сумма чисел в каждом квадрате $3\times 3$ была отрицательной, а сумма всех чисел в таблице $n\times n$ была положительной, если а) $n=5$; б) $n=6$?
комментарий/решение(2)
комментарий/решение(2)
Задача №2. Мама дала Мурату денег на 30 карандашей. Оказалось, что в магазине карандашная фабрика проводит рекламную акцию: в обмен на чек о покупке набора из 20 карандашей возвращают $25\%$ стоимости набора, а в обмен на чек о покупке набора из 5 карандашей $10\%$. Какое наибольшее число карандашей может купить Мурат?
комментарий/решение(1)
комментарий/решение(1)
Задача №3. Асан считает, что дроби «сокращают», зачеркивая одинаковые цифры в числителе и знаменателе. Марат заметил, что иногда Асан получает верные равенства, например, $\dfrac{49}{98}=\dfrac{4}{8}$. Найдите все правильные дроби с числителем и знаменателем, состоящими из двух ненулевых цифр, которые можно так «сократить».
комментарий/решение
комментарий/решение
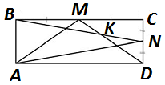
Задача №4. В прямоугольнике $ABCD$ отмечены точка $M$ — середина стороны $BC$, точка $N$ — середина стороны $CD$, точка $K$ — точка пересечения отрезков $BN$ и $MD$ (см. рис.). Докажите, что $\angle MKB=\angle MAN$.
комментарий/решение(2)
комментарий/решение(2)
Задача №5. Средний возраст одиннадцати футболистов — 22 года. Во время игры один из игроков получил травму и ушел с поля. Средний возраст оставшихся игроков стал 21 год. Сколько лет футболисту, ушедшему с поля?
комментарий/решение(1)
комментарий/решение(1)
Задача №6. Женя и Антон учатся в одном классе. У Антона одноклассников вчетверо больше, чем одноклассниц. А у Жени одноклассниц на 17 меньше, чем одноклассников. Кто Женя: девочка или мальчик?
комментарий/решение(1)
комментарий/решение(1)
Задача №7. Имеется 10 отрезков, длины которых выражаются попарно различными натуральными числами, не превосходящими 80. Докажите, что среди этих отрезков найдутся три, из которых можно составить треугольник.
комментарий/решение(1)
комментарий/решение(1)
Задача №8. В прямоугольном треугольнике $ABC$ проведены биссектрисы $AP$ и $BQ$ из вершин острых углов. Точки $D$ и $E$ — основания перпендикуляров опущенных из $Q$ и $P$ на гипотенузу$AB$. Найдите угол $DCE$.
комментарий/решение(1)
комментарий/решение(1)