Эйлер атындағы олимпиада, 2014-2015 оқу жылы, аймақтық кезеңнің 2 туры
Есеп №1. Үстелде ұзындығы 10 см болатын таяқ жатыр. Петя оны екі бөлікке бөліп пайда болған екі бөлікті де үстелге қояды. Үстелде жатқан тяқтардың біреуіне Вася да сондай операция қолданады, сосын сондай операцияны Петя да жасайды және т.с.с. кезектесе береді. Петя 18 бөлуден кейін пайда болған барлық таяқшалар 1 см-ден қысқа болғанын қалайды. Ал Вася Петяға кедергі келтіргісі келеді. Қарсыласының ісіне қарамастан, балалардың қайсысында өз мақсатына жетуіне мүмкіндігі бар?
(
И. Рубанов,
С. Берлов
)
комментарий/решение(1)
комментарий/решение(1)
Есеп №2. Көрермендер фильмді 0-ден 10-ға дейінгі бүтін ұпаймен бағалайды. Уақыттың әр мезетінде фильмнің рейтингі оған дейін қойылған ұпайлардың қосындысын сол ұпайлар санына бөлу арқылы есептелінеді. Қандай да бір $T$ уақытта рейтинг бүтін сан болған, сосын жаңадан дауыс берген көрерменнен кейін ол рейтинг 1 ұпайға азайып отырған. $T$ уақыттан кейін ең көп дегенде қанша көрермен дауыс беруі мүмкін?
(
Р. Женодаров,
О. Дмитриев
)
комментарий/решение(1)
комментарий/решение(1)
Есеп №3. $ABCD$ трапециясында $(AD \parallel BC)$, $B$ бұрышы $A$ мен $D$ бұрыштарының қосындысына тең. $CD$ кесіндісінің $D$ төбесінен әрі қарай созындысынан $DK=BC$ болатындай кесінді жүргізілген. $AK=BK$ екенін дәлелдеңіздер.
(
Б. Обухов
)
комментарий/решение(1)
комментарий/решение(1)
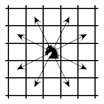
Есеп №4. Өлшемі $20 \times 20$ болатын шахмат тақтасына, барлық бос шаршылар ұрылатындай, 220 ат фигурасы қойылған. Бұрынғы шаршылармен қоса алғанда, пайда болған бос шаршылар да ұрылатындай, тақтадан 20 ат фигурасын алып тастауға болатынын дәлелдеңдер. Ат фигурасы «Г» әріпімен ұратынын естеріңізге саламыз (суретті қара).
комментарий/решение(1)
комментарий/решение(1)