7-я олимпиада им. Шалтая Смагулова, 6 класс, 2 тур

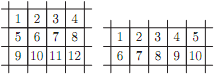
Задача №1. На плоскости разрешается проводить горизонтальные и вертикальные линии. С помощью 9 таких линии можно получить как 12 клеток, взяв 4 горизонтальных и 5 вертикальных, так и 10 клеток, взяв 3 горизонтальных и 6 вертикальных (см. рис.). Какое наибольшее количество клеток можно получить из 15 прямых?

комментарий/решение

Задача №2. Используя несколько ненулевых цифр, составили всевозможные двухзначные числа. Докажите, что сумма всех этих двухзначных чисел делится на 11.
комментарий/решение

Задача №3. Про натуральное число

$n$ сделано шесть утверждений:

$3 n > 91; \quad n < 120; \quad n < 27; \quad 4n > 37; \quad 2n \geq 21; \quad n > 7.$ Известно, что только три из них верны, а три неверны. Найдите число

$n$ .
комментарий/решение

Задача №4. Караван верблюдов везет в большой бочке весь запас питьевой воды. В бочке оказалась дырочка, сквозь которую вода незаметно с постоянной скоростью сочится в песок. Если бы в караване было бы 10 всадников, то воды им хватило бы на 10 дней, а если бы было 8 всадников — то на 12 дней. На самом деле всего было 4 всадника. На сколько дней им хватит воды, если известно, что воду пьют только всадники?
комментарий/решение

Задача №5. В строку последовательно выписывают 101 чисел по следующему правилу: первое число равно 1, а каждое следующее, начиная со второго, или на 2 меньше предыдущего числа, или в 3 раза больше предыдущего числа. Могло ли оказаться так, что сумма всех 101 чисел равна
а) 2024;
б) 2023?
комментарий/решение(1)