7-я олимпиада им. Шалтая Смагулова, 6 класс, 2 тур

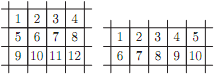
Есеп №1. Жазықтықта горизонталь мен вертикаль түзу жүзгізуге рұқсат. Осындай 9 түзу арқылы, оның 4-еуін горизонталь және 5-еуін вертикаль етіп алып, 12 ұяшық та ала аламыз, және оның 3-еуін горизонталь және 6-ын вертикаль етіп алып, 10 ұяшық та ала аламыз (суретті қара). Осындай 15 түзудің көмегімен ең көп дегенде неше ұяшық ала аламыз?

комментарий/решение

Есеп №2. Нөлден өзгеше бірнеше цифрларды қолданып, барлық мүмкін екі таңбалы сандар құрастырылды. Осы барлық құрастырылған сандардың қосындысы 11-ге бөлінетін дәлелдеңіз.
комментарий/решение

Есеп №3. Натурал $n$ саны үшін алты тұжырым жасалды: $$ 3 n > 91; \quad n < 120; \quad n < 27; \quad 4n > 37; \quad 2n \geq 21; \quad n > 7. $$ Тек үш тұжырым дұрыс, ал үшеуі қате екені белгілі. $n$ санын табыңыз.
комментарий/решение

Есеп №4. Түйе керуені ауыз суды үлкен бөшкеге алып келе жатыр. Бөшкеде кішкентай саңылау болған, сондықтан саңылау арқылы су аз-аздан тұрақты жылдамдықпен құмға төгіледі. Егер керуенде 10 адам болса, оларға су 10 күнге, ал егер 8 адам болса, 12 күнге жетуші еді. Негізінде барлығы 4 адам болған. Осы 4 адамға су неше күнге жетеді? (Суды тек адамдар ғана ішеді.)
комментарий/решение

Есеп №5. Тізбекке 101 санды келесі ережені сақтай отыра бірінен кейін бірін жазады: бірінші сан 1-ге тең, ал әр келесі сан (екінші саннан бастап есептегенде) оған дейін тұрған саннан 2-ге кем немесе оған дейін тұрған саннан 3 есе артық. Осы жазылған 101 санның қосындысы
   а) 2024-ке;
   б) 2023-ке
   тең бола алады ма?
комментарий/решение