Городская Жаутыковская олимпиада по математике, 6 класс, 2021 год

Задача №1. В комнате сидят 25 человек. Каждый из них либо рыцарь, либо лжец, либо хитрец. Каждому задали подряд три вопроса: «Ты рыцарь?», «Ты хитрец?», «Ты лжец?». На первый вопрос ответ «Да» дали 17, на второй — 12, на третий — 8 человек. Сколько хитрецов в комнате? Рыцари всегда говорят правду, лжецы — всегда ложь, хитрецы — иногда правду, иногда ложь.
комментарий/решение

Задача №2. Последовательные нечетные числа записаны в клетки строк квадратной таблицы по определенному правилу (смотри рисунок). Найдите сумму всех записанных в эту таблицу чисел.

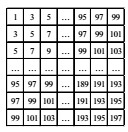
комментарий/решение

Задача №3. Принцесса Жвачка приготовила капкейки. Финн пришел в Империю Сласти и съел сперва один, затем четверть от всех оставшихся. Потом в Империю Сласти пришел Джейк, и тоже съел сперва один капкейк, а потом четверть всех оставшихся. А потом Принцесса Жвачка пришла и обнаружила, что осталось больше 50, но меньше 60 капкейков. Сколько капкейков приготовила Принцесса изначально? (После каждого съедания должно оставаться целое число капкейков.)
комментарий/решение

Задача №4. На плоскости проведено несколько прямых. Для каждой прямой подсчитали число прямых, которые она пересекает, и записали рядом с данной прямой. Может ли сумма всех записанных чисел равняться а) 99; б) 100?
комментарий/решение

Задача №5. На доске написаны целые числа от 1 до 10. Мальчик хочет стереть несколько из них так, чтобы произведение оставшихся не делилось на 6. Какое наименьшее количество чисел ему придется стереть?
комментарий/решение

Задача №6. Можно ли на прямой отметить точки $A$, $B$, $C$, $D$, $E$ так, чтобы расстояния между ними в сантиметрах оказались равны: $AB = 6$, $BC = 7$, $CD = 10$, $DE = 9$, $AE = 12$?
комментарий/решение

Задача №7. На доске написаны числа 20, 20, 20, 21. Разрешается либо умножить любое число на 3 и результат записать на доске вместо исходного числа, либо прибавить к любым двум числам на доске 1 и записать полученные числа вместо исходных. Можно ли в результате этих операций получить четыре числа, произведение которых будет равно 20202021?
комментарий/решение

Задача №8. Каждый робот имеет три ручки и несколько антенн. Каждый робот взял за руки трех других (так что все руки оказались заняты). Оказалось, что у любых двух роботов, взявшихся за руки, количество антенн отличается ровно в шесть раз. Может ли суммарное количество антенн у роботов быть равно 2021?
комментарий/решение