Городская Жаутыковская олимпиада по математике, 6 класс, 2021 год

Есеп №1. Бөлмеде 25 адам бар. Олардың әрқайсысы немесе сері, немесе өтірікші, немесе қу. Олардың әрқайсысына қатарынан үш сұрақ қойылды: «Сен серісің ба?», «Сен қусың ба?», «Сен өтірікшісің бе?». Бірінші сұраққа «Иә» деп 17 адам, екінші сұраққа 12 адам, үшінші сұраққа 8 адам жауап берді. Бөлмеде неше қу адам бар? Серілер әрқашан шындықты айтады, өтірікшілер әрқашан өтірік айтады, қулар — кейде шындықты, кейде өтірік айтады.
комментарий/решение

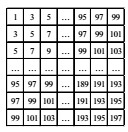
Есеп №2. Қатар келген тақ сандар белгілі бір ереже бойынша шаршы қатарының клеткаларына жазылған (суретті қараңыз). Осы шаршының клеткаларына жазылған барлық сандардың қосындысын табыңыз.

комментарий/решение

Есеп №3. Тәтті Империяда Сағыз Ханшайымы капкейктерді пісірді. Финн Тәтті Империяға келіп алдымен бір капкейкті, кейін қалғандарының төрттен бірін жеп қойды. Одан кейін Джейк келіп алдымен біреуін, кейін қалғандарының төрттен бірін жеп қойды. Сағыз Ханшайымы қайтып келген кезде капкейктердің саны 50-ден көп, бірақ 60-тан аз екенін байқады. Ең басында Ханшайым қанша капкейк пісірді? (Капкейктерді әрбір жеу кезінен кейін, олардың саны бүтін болып отыру керек.)
комментарий/решение

Есеп №4. Жазықтықта бірнеше түзулер жүргізілген. Әр түзудің жанына сол түзу қиып өтетін түзулердің санын жазған. Барлық жазылған сандардың қосындысы
   а) 99-ға;
   б) 100-ге
   тең бола ала ма?
комментарий/решение

Есеп №5. Тақтаға 1-ден 10-ға дейін бүтін сандар жазылған. Қалғандарының көбейтіндісі 6-ға бөлінбейтіндей етіп, тақтадағы сандардың бірнешеуін өшіру керек. Ол үшін тақтадағы сандардың кемінде қаншасын өшіру керек?
комментарий/решение

Есеп №6. Бір түзудің бойынан $AB = 6$ см, $BC = 7$ см, $CD = 10$ см, $DE = 9$ см, $AE = 12$ см болатындай етіп, $A$, $B$, $C$, $D$, $E$ нүктелерін белгілеуге болады ма?
комментарий/решение

Есеп №7. Тақтада 20, 20, 20, 21 сандары жазылған. Бір операцияда кез келген санды 3-ке көбейтіп, нәтижені бастапқы санның орнына жазуға, немесе тақтадағы кез келген екі санға 1-ді қосып, қосындыны сол екі санның орнына жазуға рұқсат етіледі. Осы операциялардың көмегімен көбейтіндісі 20202021-ге тең төрт сан алуға болады ма?
комментарий/решение

Есеп №8. Әрбір роботтың үш қолы және бірнеше антеннасы бар. Әрбір робот басқа үш қолды ұстады (барлық қолдар бос болу үшін). Кез келген қол ұстасқан екі роботтың біреуінің антенна саны екіншісінікінен дәл 6 есе көп екені белгілі. Барлық роботтардың антенналардың жалпы саны 2021-ге тең болуы мүмкін бе?
комментарий/решение