Городская Жаутыковская олимпиада по математике, 7 класс, 2020 год
Задача №1. Для чисел $a,$ $b,$ $c$ выполняются равенства $(a+b)(a+b+c)=5,$ $(b+c)(b+c+a)=6$ и $(c+a)(c+a+b)=7.$ Вычислите значение выражения ${(a+b+c)}^3.$
комментарий/решение(3)
комментарий/решение(3)
Задача №2. На рисунке ниже даны 5 фигур, пронумерованные от 1 до 5. Известно, что используя ровно четыре фигуры из пяти, сложили квадрат. Напишите номер фигуры, которая не использовалась.
комментарий/решение
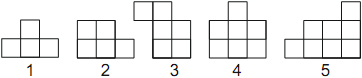
комментарий/решение
Задача №3. Здание разделено на 9 прямоугольных комнат. Измерили периметры шести комнат. Пять из шести результатов измерений показаны на рисунке снизу, а результат шестого обозначен буквой $x$. Чему равен $x?$
комментарий/решение
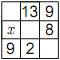
комментарий/решение
Задача №4. В коробке лежат шары, их меньше 100. Среди них есть зеленые и красные. Количество зелёных составляет $12\%$, а количество красных — $18\%$ от общего количества шаров. Сколько всего шаров лежат в коробке?
комментарий/решение(1)
комментарий/решение(1)
Задача №5. Два равносторонних треугольника с периметрами 17 и 19, расположены так, что их стороны соответственно параллельны. Найдите периметр образовавшегося шестиугольника.
комментарий/решение
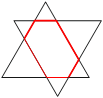
комментарий/решение
Задача №6. Пусть $S=\frac{1}{{x(x + 1)}}+ \frac{1}{{(x + 1)(x + 2)}}+ \ldots + \frac{1}{{(x + 4)(x + 5)}}.$ Найдите $[S]$ при $x=\frac{2}{11}$. Здесь $[t]$ означает целую часть числа $[t]$, то есть наибольшее целое число, не превосходящее $t$. Например, $[3,85]=3$.
комментарий/решение
комментарий/решение
Задача №7. Найдите количество натуральных $n$ таких, что $1 \le n \le 100$ и дробь $\frac{3n^2-26n+35}{4n-28}$ является целым числом.
комментарий/решение(1)
комментарий/решение(1)
Задача №8. Пусть $a, b, c$ и $d$ такие натуральные числа, что $\text{НОД}(a, b)=24$, $\text{НОД}(b, c)=36$, $\text{НОД}(c, d)=54$, $70 < \text{НОД}(d, a) < 100$. Найдите наибольший простой делитель числа $a.$
комментарий/решение
комментарий/решение
Задача №9. На рисунке ниже известно, что $CD$ параллелен $BE$. Скольким градусам равен $a$?
комментарий/решение
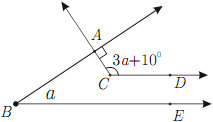
комментарий/решение
Задача №10. В треугольнике $ABC$, где $AB = AC$, биссектриса $AM$ в два раза короче биссектрисы $BD.$ Скольким градусам равен угол $ABC$?
комментарий/решение
комментарий/решение