Городская Жаутыковская олимпиада по математике, 7 класс, 2020 год
Есеп №1. $a,$ $b,$ $c$ сандары келесі үш теңдікті қанағаттандырады: $(a+b)(a+b+c)=5,$ $(b+c)(b+c+a)=6,$ $(c+a)(c+a+b)=7$. ${(a+b+c)}^3$ өрнегінің мәнін табыңыз.
комментарий/решение(3)
комментарий/решение(3)
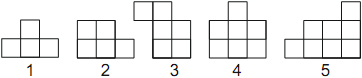
Есеп №2. Төменді суретте 1-ден 5-ке дейін нөмірленген бес фигура көрсетілген. Осы фигуралардың дәл төртеуін қолданып, шаршы құрастырған. Кұрастыру кезінде қай фигура қолданылмады? Жауабында фигура нөмірін жазыңыз.
комментарий/решение
комментарий/решение
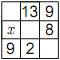
Есеп №3. Үйдің бір үлкен бөлмесі 9 кіші тіктөртбұрышты бөлмелерге бөлінген. Алты бөлменің периметрлері өлшенді. Алты өлшемнің бесеуі суретте көрсетілген, ал алтыншысының өлшемі $x$ арқылы берілген. $x$ нешеге тең?
комментарий/решение
комментарий/решение
Есеп №4. Қорапта шарлар бар. Шарлар саны 100-ден кем. Шарлар арасында жасыл шарлар бар, олардың саны барлық шар санының $12\%$ -ын құрайды, және қылыл шарлар бар, олардың саны барлық шар санының $18\%$-ын құрайды. Қорапта барлығы қанша шар бар?
комментарий/решение(1)
комментарий/решение(1)
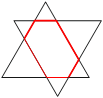
Есеп №5. Периметрлері 17-ге және 19-ға тең екі теңқабырғалы үшбұрыштардың сәйкес қабырғалары параллель. Осы екі үшбұрыш алтыбұрышты шектейді. Сол алтыбұрыштың периметрін анықтаңыз.
комментарий/решение
комментарий/решение
Есеп №6. $S=\frac{1}{{x(x + 1)}}+ \frac{1}{{(x + 1)(x + 2)}}+ \ldots + \frac{1}{{(x + 4)(x + 5)}}$ болсын. $x=\frac{2}{11}$ болғанда $[S]$-ті табыңыз. Бұл жерде $[t]$ арқылы санының бүтін бөлігі белгіленген, яғни $[t]$ дегеніміз $t$-дан аспайтын ең үлкен бүтін сан. Мысалға $[3,85]=3$.
комментарий/решение
комментарий/решение
Есеп №7. $1 \le n \le 100$ және $\frac{3n^2-26n+35}{4n-28}$ бөлшегі бүтін сан болатындай қанша натурал $n$ саны бар?
комментарий/решение(1)
комментарий/решение(1)
Есеп №8. $\text{ЕҮОБ}(a, b)=24$, $\text{ЕҮОБ}(b, c)=36$, $\text{ЕҮОБ}(c, d)=54$, $70 < \text{ЕҮОБ}(d, a) < 100$ болатындай $a, b, c$ және $d$ натурал сандары берілсін. $a$ санының ең үлкен жай бөлгішін табыңыз.
комментарий/решение
комментарий/решение
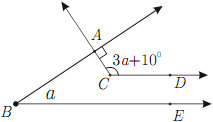
Есеп №9. Төмендегі суретте $CD$ және $BE$ параллель болса, $a$ саны қанша градусқа тең?
комментарий/решение
комментарий/решение
Есеп №10. $ABC$ үшбұрышында $AB = AC$ және үшбұрыштың $AM$ биссектрисасы $BD$ биссектрисадан екі есе қысқа. $ABC$ бұрышы неше градусқа тең?
комментарий/решение
комментарий/решение