6-я олимпиада им. Шалтая Смагулова, 6 класс, 1 тур

Задача №1. В окружность радиусом 20 вписан квадрат (см. рис.). Найдите сумму площадей закрашенных частей. Считайте, что $\pi = 3,\!14$.

комментарий/решение(2)

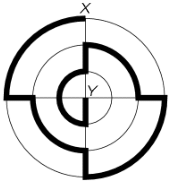
Задача №2. На рисунке даны три круга радиусов 100 см, 200 см и 300 см, имеющие общий центр. Мышка пробежала из края большого круга (точки $X$) до центра (до точки $Y$) по выделенной жирной траектории. Сколько сантиметров пробежала мышка? Считайте, что $\pi = 3,\!14$.

комментарий/решение(2)

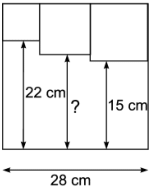
Задача №3. Внутри квадрата расположены три меньших квадрата так, как показано на рисунке . Скольким сантиметрам равна длина отрезка, обозначенного знаком вопроса?

комментарий/решение(2)

Задача №4. Когда в примере разности чисел некоторые цифры заменили звездочкой, то получилось: $1*3*2-649*=8*95$. Чему равна сумма цифр, замененных звездочками?
комментарий/решение(1)

Задача №5. На какое число поделили число 2023, если в частном получилось 43, а в остатке 2?
комментарий/решение(1)

Задача №6. Найдите натуральное число $n$ такое, что выполнены неравенства $2,5 < 3\frac{5}{{12}} - \frac{n}{4} < 2\frac{5}{6}$.
комментарий/решение(2)

Задача №7. Щенок Армана выпивает 6 чашек молока в день, а 5 литров молока, как известно, стоит 1500 тг. Если вместимость чашки 250 мл, на сколько тенге Арман должен купить молоко для щенка на 10 дней?
комментарий/решение(2)

Задача №8. В турнире участвуют 16 шахматистов, где каждый игрок должен играть с каждым другим ровно один раз. В некоторый момент времени из сыгранных партий Асан имел половину выигрышей, треть проигрышей и 2 ничьих. Сколько партий ещё оставалось сыграть Асану?
комментарий/решение(2)

Задача №9. Каждую задачу по геометрии Арман решает за 3 минуты, а Талгат — за 5 минут. Каждую логическую задачу Арман решает за 9 минут, а Талгат — за 7 минут. За какое наименьшее время (в минутах) Арман и Талгат вместе решат 9 геомертических и 5 логических задач? (Каждую задачу они решают индивидуально.)
комментарий/решение(1)

Задача №10. Пусть $A = 1! + 2! + 3! + \ldots + 2023!$. Вычислите остаток от деления $A$ на 100. Как обычно, через $n!$ обозначется произведение всех натуральных чисел от 1 до $n$.
комментарий/решение(2)

Задача №11. Если сложить количество зайцев и волков в лесу, то сумма будет в 5/3 раза больше количества медведей и на 1 больше количества птиц. Если 7/8 количества ног волков равно количеству зайцев, а сумма количества ног медведей и количество ушей зайцев в 4 раза больше, чем количество птиц, то сколько медведей в лесу?
комментарий/решение(3)

Задача №12. Два малыша делились конфетами. Сначала первый дал половину своих конфет (отдал второму), потом второй дал половину своих первому, потом снова первый дал половину своих. В результате у первого оказалось 15 конфет, а у второго — 33. Сколько конфет было у первого в начале?
комментарий/решение(2)

Задача №13. Найдите сумму всех трехзначных чисел, цифры которых не повторяются.
комментарий/решение

Задача №14. Среди всех 10-значных чисел, цифры которых не повторяются и делятся на 36, пусть $A$ — наибольшее, а $B$ — наименьшее. Найдите сумму $A + B$.
комментарий/решение(1)

Задача №15. В ряд выписали числа в порядке 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 и перед каждым числом записали знаки «$+$» или «$-$».Тогда значение выражения оказалось равным 7. Какова сумма чисел, стоящих после знаков плюс?
комментарий/решение(1)

Задача №16. Сколько существует натуральных пар $(X,Y)$ таких, что $\text{НОД}(X,Y)=8$ и $X \cdot Y = 384$?
комментарий/решение(1)

Задача №17. Запишите наибольшее четырехзначное число, первые две цифры которого меньше суммы двух последних цифр.
комментарий/решение(1)

Задача №18. Даны числа 1, 2, 3, $\ldots$, 2023. Сколько из этих чисел имеют не менее трех одинаковых цифр?
комментарий/решение(1)

Задача №19. В клетчатом прямоугольнике $20\times 23$ произвольным образом закрасили 4 строки и 4 столбца. Сколько всего клеток закрасили?
комментарий/решение(5)

Задача №20. Если $c\ne 0$, $a+b+d=m\cdot n$, $n\cdot c=a$ и $b\cdot c+d\cdot c+4c=m\cdot a$ то, найти значение $a$.
комментарий/решение(2)