6-я олимпиада им. Шалтая Смагулова, 6 класс, 1 тур
Есеп №1. Радиусы 20-ға тең шеңберге суреттегідей, іштей шаршы сызылған. Боялған бөліктің ауданын тап. $\pi = 3,\!14$ деп есептеңіздер.
комментарий/решение(2)

комментарий/решение(2)
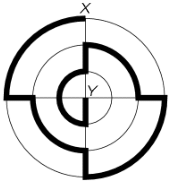
Есеп №2. Суретте радиустары 100 см, 200 см және 300 см болатын, ортақ центрі бар үш шеңбер көрсетілген. Тышқан үлкен шеңбердің шетінен ($X$ нүктесі) оның ортасына ($Y$ нүктесіне дейін) белгіленген қалың жол бойымен жүрді. Тышқан неше сантиметр жүрген? $\pi = 3,\!14$ деп есептеңіздер.
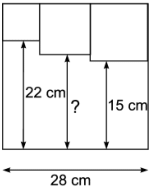
Есеп №3. Шаршының ішінде суретте көрсетілгендей үш кішірек шаршы бар. Сұрақ белгісімен көрсетілген кесіндінің ұзындығы неше сантиметрге тең?
комментарий/решение(2)
комментарий/решение(2)
Есеп №4. Сандарды азайту мысалында кейбір цифрлар жұлдызшамен ауыстырылған кезде, $1*3*2-649*=8*95$ мысалы шыққан. Жұлдызшамен ауыстырылған цифрлардың қосындысы нешеге тең?
комментарий/решение(1)
комментарий/решение(1)
Есеп №6. $2,5 < 3\frac{5}{{12}} - \frac{n}{4} < 2\frac{5}{6}$ теңсіздіктері орындалатындай натурал $n$ санын табыңыз.
комментарий/решение(2)
комментарий/решение(2)
Есеп №7. Арманның күшігі күніне 6 кесе сүт ішеді, ал 5 литр сүттің бағасы 1500 тг екені белгілі. Егер бір кесеге 250 мл сүт сиятын болса, Арман күшігіне 10 күнге неше теңгеге сүт алауы керек?
комментарий/решение(2)
комментарий/решение(2)
Есеп №8. Турнирге 16 шахматшы қатысады, онда әр ойыншы әрбірімен дәл бір рет ойнауы керек. Белгілі бір уақытта Асан ойнаған ойындардың ішінде жартысы жеңіс, үштен бірі жеңіліс және 2 тең ойыны болды. Асанға жарысты аяқтау үшін әлі неше ойын ойнауы кажет?
комментарий/решение(2)
комментарий/решение(2)
Есеп №9. Геометрияның әр есебін Арман 3 минутта, Талғат 5 минутта шығарады. Ал логикалық әр есепті Арман 9 минутта, Талғат 7 минутта шығарады. Арман мен Талғат бірлесіп, 9 геометрияның және 5 логикалық есепті ең жылдам дегенде неше минутта шығарады? (Бір есепті тек бір адам шығарады.)
комментарий/решение(1)
комментарий/решение(1)
Есеп №10. $A = 1! + 2 ! + 3! + \ldots + 2023!$. $A$–ның, 100-ге бөлгендегі қалдығын есепте. Әдеттегідей, $n!$ деп алдыңғы $n$ натурал санның көбейтіндісін белгілейміз.
комментарий/решение(2)
комментарий/решение(2)
Есеп №11. Ормандағы қояндар мен қасқырлардың санын қоссақ, қосынды аюлардын санынан 5/3 есе, ал құстардың санынан 1-ге артық болады. Егер қасқырлардың аяқтарының санының 7/8 бөлігі қояндар санына тең және аюлардың аяқтарының саны мен қоянның құлақтарының санын қосқанда, құстардың санынан 4 есе артық болған болса, орманда қанша аю бар?
комментарий/решение(3)
комментарий/решение(3)
Есеп №12. Екі бала бір-бірімен кәмпит бөлісті. Алдымен, біріншісі өзінің кәмпиттерінің жартысын екіншісіне берді, содан кейін екіншісі өзінің кәмпиттерінің жартысын біріншіге берді, содан кейін біріншісі өзінің кәмпиттерінің жартысын екіншіге берді. Нәтижесінде біріншісінде 15 кәмпит болды, ал екіншісінде 33. Біріншісінде басында неше кәмпит болды?
комментарий/решение(2)
комментарий/решение(2)
Есеп №14. Цифрлары қайталанбайтын және 36-ға бөлінетін бардық 10 таңбалы сандардың ішінде, ең үлкенін $A$ дейік, ең кішісін $B$ дейік. $A+B$ қосындысы нешеге тең?
комментарий/решение(1)
комментарий/решение(1)
Есеп №15. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 сандарын осы ретпен бір қатарға тізіп шығып, әр санның алдына «$+$» немесе «$-$» таңбаларын қойды. Сол кезде өрнектің мәні 7-ге тең болып шыққан. Сонда тек қосу таңбаларынан кейін тұрған сандардың қосындысы нешеге тең?
комментарий/решение(1)
комментарий/решение(1)
Есеп №16. $\text{ЕҮОБ}(X, Y) = 8$ және $X \cdot Y = 384$ теңдеулерін қанағаттандыратын, қанша $(X, Y)$ натурал сандар жұбы бар? (ЕҮОБ — ең үлкен ортақ бөлгіш.)
комментарий/решение(1)
комментарий/решение(1)
Есеп №17. Алдыңғы екі цифры соңғы екі цифрының қосындысынан кіші болатындай ең үлкен төрт таңбалы сан жазыңыз.
комментарий/решение(1)
комментарий/решение(1)
Есеп №18. 1, 2, 3, $\ldots$ 2023 сандары берілген. Осы сандардың ішінде кем дегенде бірдей үш цифры бар болатын неше сан бар?
комментарий/решение(1)
комментарий/решение(1)
Есеп №19. Өлшемі $20\times 23$ болатын ұяшықты тіктөртбұрышта 4 жол және 4 баған кездейсоқ боялған. Барлығы неше ұяшық боялған?
комментарий/решение(5)
комментарий/решение(5)
Есеп №20. Егер $c\ne 0$, $a+b+d=m\cdot n$, $n\cdot c=a$ және $b\cdot c+d\cdot c+4c=m\cdot a$ болса, $a$–ның мәнін тап.
комментарий/решение(2)
комментарий/решение(2)