Городская Жаутыковская олимпиада по математике, 8 класс, 2018 год

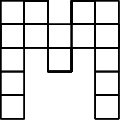
Есеп №1. Төмендегі суретте көрсетілген фигураны бірдей неше бөлікке бөлуге болады? Барлық мүмкін жағдайларды қарастырыңыз. (Егерде бір бөліктің біреуін екінші бөлікті айналдыру немесе бұру арқылы алуға болатын болса, ондай бөліктерді бірдей деп санаймыз. Фигураны тек кесте сызықтарының бойымен ғана қиюға болады.)

комментарий/решение

Есеп №2. Кез келген тақ

$a,$

$b$ және

$c$ сандары үшін

$ab(a-b)+bc(b-c)+ca(c-a)$ өрнегі 16-ға бөлінетінін дәлелдеңіз.
комментарий/решение(3)

Есеп №3.

$ABCD$ дөңес төртбұрышында:

$\angle ABC=140^\circ$ ,

$\angle ADC=115^\circ$ ,

$\angle CBD=40^\circ$ ,

$\angle CDB=65^\circ$ екені белгілі.

$\angle ACD$ бұрышы неше градусқа тең?
комментарий/решение(1)

Есеп №4.

$2^n > n^{2018}$ теңсіздігі орындалатындай

$n > 1$ натурал саны табылады ма? Жауабыңызды негіздеңіз.
комментарий/решение(1)

Есеп №5. Шеңберде
а) 20 хорда;
б) 19 хорда жүргізілген.
Олардың ешбір үшеуі бір нүктеде қиылыспайды және ешбір екеуі бір нүктеден шықпайды. Олардың барлық қиылысу нүктелерін белгілейік. Белгіленген нүктелер саны 100-ге тең бола алады ма?
комментарий/решение

Есеп №6.

$a,$

$b$ және

$c$ сандарының кез келген екеуінің көбейтіндісі үшіншісіне тең емес. Егерде

$a+b+c=1$ болса, келесі теңдікті дәлелдеңіз:

$\left( {\frac{1}{{a - bc}} + \frac{1}{{b - ac}} + \frac{1}{{c - ab}}} \right)\left( {a - bc} \right)\left( {b - ac} \right)\left( {c - ab} \right) = 4abc.$
комментарий/решение(1)

Есеп №7. Дәл 25-і бүтін толық квадрат болатындай 2018 қатар келген натурал сан бар екенін дәлелдеңіз.
комментарий/решение(1)

Есеп №8. Радиустары 3, 4 және 5-ке тең үш шоғырлас (центрлері ортақ) шеңберлер берілген. Радиусы 5-ке тең шеңбердің өзара қиылысатын

$AB$ және

$CD$ хордалары, сәйкесінше радиустары 3 және 4-ке тең шеңберлерді жанайды.

$AC$ және

$BD$ түзулері тік бұрыш жасап қиылысатын дәлелдеңіз.
комментарий/решение(3)