Геометриядан Иран олимпиадасы, 2017 жыл, 1-ші лига (7-8 сыныптар)

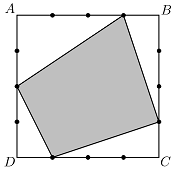
Есеп №1. Қабырғасы 4 болатын $ABCD$ шаршысының әр қабырғасы үш нүктемен төрт тең кесіндіге бөлінген (төменгі сур. қара). Квадраттың әр қабырғасынан белгіленген төрт нүктенің біреуін таңдап алған. Таңдап алынған нүктелерді тізбектеп төртбұрыш шығатындай қосқан. Сол төртбұрыштың ауданы неге тең болуы мүмкін? Барлық мүмкін жауапты жазыңыздар, жауаптарды негіздеудің қажеті жоқ.

комментарий/решение(2)

Есеп №2. Төменгі суретте $ABC$ үшбұрышының бұрыштарын табыңыздар.

комментарий/решение(2)

Есеп №3. Дұрыс $ABCDE$ бесбұрышы берілген. $CD$ түзуіне $C$ нүктесінде тұрғызылған перпендикуляр $AB$ түзуін $F$ нүктесінде қиса, $AE+AF=BE$ теңдігін дәлелдеңіздер.
комментарий/решение(1)

Есеп №4. Ешбір үшеуі бір түзудің бойында жатпайтындай жазықтықта $P_1$, $P_2, \ldots, P_{100}$ нүктелері берілген. Кез келген $P_i$, $P_j$, $P_k$ $(i < j < k)$ үштіктері үшін осы нүктелерден құралатын үшбұрышты дұрыс бағытталған деп атайық, егер $P_i$ нүктеден $P_iP_j$, $P_jP_k$, $P_kP_i$ кесінділерін айналып өту сағат бағытымен бағыттас болса. Дұрыс бағытталған үшбұрыштардың саны дәл 2017-ге тең бола алады ма?
комментарий/решение

Есеп №5. Теңбүйірлі $ABC$ ($AB=AC$) үшбұрышы берілген. $l$ түзуі $A$ нүктесі арқылы өтетін және $BC$-ға параллель түзу. $D$ — $l$ түзуінде кез келген белгіленген нүкте болсын. $E$ және $F$ нүктелері $A$ нүктесінен сәйкесінше $BD$ және $CD$ түзулеріне түсірілген перпендикулярлар табандары. $P$ және $Q$ нүктелері сәйкесінше $E$ және $F$ нүктелерінен $l$-ге түсірілген перпендикулярлар табандары. $AP+AQ \leqslant AB$ теңсіздігін дәлелдеңіздер.
комментарий/решение(1)