Леонард Эйлер атындағы олимпиада,
2010-2011 оқу жылы, қорытынды кезеңнің 2-ші туры

Есеп №1. Қатарынан келетін 100 натурал сандарды цифрларының қосындысы өсуі бойынша, ал қосындысы тең болатын сандар үшін сол сандардың өсуі бойынша сорттады. 2010 мен 2011 сандары бірге келе алады ма? ( С. Волчёнков )
комментарий/решение(1)

---

Есеп №2. $AB \parallel CD$, $BC \parallel AD$, $AC \parallel DE$, $CE \perp BC$ болатындай $ABCDE$ дөңес бесбұрышы берілген. $EC$ — $BED$ бұрышының биссектрисасы болатынын дәлелдеңіз. ( П. Кожевников )
комментарий/решение(1)

---

Есеп №3.  Шеңбер бойымен қысқартылмайтын бөлімі тақ және $10^{10}$ үлкен болатындай бес қызыл бөлшек жазды. Әрбір көршілес қызыл бөлшек арасына қысқартылмайтын екеуінінің көк қосындысын жазды. Барлық көк бөлшектердің бөлімдері 100 ден кіші болуы мүмкін бе? ( И. Богданов )
комментарий/решение(2)

---

Есеп №4. $9 \times 9$ тор көзді тақтаға ең көп дегенде бір бірін жемейтіндей(сондай ақ, өзінің түсімен бірдей пешканы) қанша қара және ақ пешка қоюға (пешка, өзінің түсіне тәуелсіз кез келген шаршыға қоюға болады) болады? Ақ пешка нөмері үлкен көршіес екі диоганальді жейді, ал қара пешка нөмері төмен екі көршілес диоганальді жейді (сур. қараңыз).

( А. Антропов )
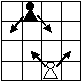
комментарий/решение(1)

---