А. Антропов
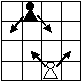
Задача №1. Какое наибольшее количество белых и чёрных пешек можно расставить на клетчатой доске $9 \times 9$ (пешку, независимо от её цвета, можно ставить на любую клетку доски) так, чтобы никакая не била никакую (в том числе и своего цвета)? Белая пешка бьет две соседние по диагонали клетки на соседней горизонтали с бoльшим номером, а чёрная — две соседние по диагонали клетки на соседней горизонтали с меньшим номером (см. рисунок).
комментарий/решение(1) олимпиада
Задача №2. В треугольнике $ABC$ сторона $AB$ больше стороны $BC$. На продолжении стороны $BC$ за точку $C$ отметили точку $N$ так, что $2BN = AB+BC$. Пусть $BS$ — биссектриса треугольника $ABC$, $M$ — середина стороны $AC$, а $L$ — такая точка на отрезке $BS$, что $ML \parallel AB$. Докажите, что $2LN = AC$. ( А. Антропов )
комментарий/решение(8) олимпиада
Задача №3. а стороне $AB$ треугольника $ABC$ выбрана точка $P$, а на сторонах $AC$ и $BC$ точки $S$ и $T$ таким образом, что $AP=AS$ и $BP=BT$. Описанная окружность треугольника $PST$ вторично пересекает стороны $AB$ и $BC$ в точках $Q$ и $R$ соответственно. Прямые $PS$ и $QR$ пересекаются в точке $L$. Докажите, что прямая $CL$ делит отрезок $PQ$ пополам. ( А. Антропов )
комментарий/решение(1) олимпиада
Задача №4. Серёжа и Таня собираются показать Маше следующий фокус. Серёжа выходит из комнаты. Маша выписывает последовательность $\left(a_1, a_2, \ldots, a_n\right)$, где все $a_k$ равны 0 или 1. После этого Таня выписывает последовательность $\left(b_1, b_2, \ldots, b_n\right)$, где все $b_k$ тоже равны 0 или 1. Далее Маша либо ничего на делает, либо говорит «Мутабор!» и заменяет обе последовательности: свою — на последовательность $\left(a_n, a_{n-1}, \ldots, a_1\right)$, а последовательность Тани — на $(1-b_n, 1-b_{n-1}, \ldots, 1-b_1).$ Последовательность Маши закрывают салфеткой, а в комнату приглашают Серёжу. Серёжа, посмотрев на последовательность Тани, должен назвать последовательность, закрытую салфеткой. Для каких $n$ Серёжа и Таня, подготовившись заранее, смогут показать такой фокус? От Серёжи не требуется определять, была ли проведена операция «Мутабор». ( А. Антропов, Т. Гизатуллин )
комментарий/решение олимпиада
Задача №5. Внутри треугольника $A B C$ нашлась такая точка $L$, что $C L=A B$ и $\angle B A C+\angle B L C=180^{\circ}$. Прямая, параллельная прямой $B C$ и проходящая через точку $L$, пересекает сторону $A C$ в точке $K$. Докажите, что $A B=B K$. ( А. Антропов )
комментарий/решение(1) олимпиада