Олимпиада имени Леонарда Эйлера2010-2011 учебный год, II тур заключительного этапа

Какое наибольшее количество белых и чёрных пешек можно расставить на клетчатой доске $9 \times 9$ (пешку, независимо от её цвета, можно ставить на любую клетку доски) так, чтобы никакая не била никакую (в том числе и своего цвета)? Белая пешка бьет две соседние по диагонали клетки на соседней горизонтали с бoльшим номером, а чёрная — две соседние по диагонали клетки на соседней горизонтали с меньшим номером (см. рисунок).

( А. Антропов )

Комментарий/решение

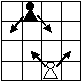
Комментарии от администратора Комментарии от администратора №1.     Ответ. 56.
Решение. Пример с 56 пешками показан на рисунке. Оценка. Заметим, что в каждом прямоугольнике из трех строк и двух столбцов стоит не более 4 пешек. Действительно, если в нем стоит хотя бы 5, то тогда на одном из цветов заняты все три клетки и пешка из центральной строки бьет одну из двух оставшихся. Следовательно, в любом прямоугольнике из 9 строк и 8 столбцов стоит не более 48 пешек (так как его можно разбить на 12 прямоугольников $3\times 2$). Допустим, нам удалось поставить 57 пешек. Тогда в девятом столбце должно стоять хотя бы 9 пешек, т.е. ровно 9. Но тогда в восьмом столбце стоит не более 2 пешек (так иначе нашлась бы пешка, стоящая не в первой и не в последней строке, которая бы била какую-то пешку из девятого столбца). Но тогда в восьмом и девятом столбцах вместе не более 11 пешек, а во 2-7 столбцах — не более 36 пешек (их можно разбить на 9 прямоугольников $3 \times 2$). Получается, что в первом столбце должно быть 10 пешек — противоречие.